
【题目】题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3()
∴a∥b()
方法二::∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3()
又∠7=∠6()
∴∠3=∠6()
∴a∥b()
方法三::∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6()
∠4+∠6=180°(平角定义)
∴a∥b()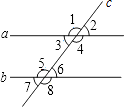
【答案】同角的补角相等;同位角相等,两直线平行;同角的补角相等;对顶角相等;等量代换;内错角相等,两直线平行;顶角相等;同旁内角互补,两直线平行
【解析】解:方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
方法二:∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
又∠7=∠6(对顶角相等)
∴∠3=∠6(等量代换)
∴a∥b(内错角相等,两直线平行)
方法三:∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6(对顶角相等)
∠4+∠6=180°(平角定义)
∴a∥b(同旁内角互补,两直线平行).
故答案是:方法一:同角的补角相等;同位角相等,两直线平行;
方法二:同角的补角相等;对顶角相等;等量代换;内错角相等,两直线平行;
方法三:对顶角相等;同旁内角互补,两直线平行.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: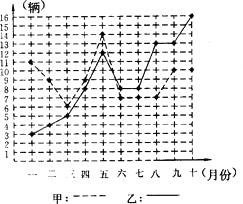
(1)请你根据上图填写下表.
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:①从平均数和方差结合看;②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两条直线相交所成的四个角中的任意一个角等于___,那么这两条直线互相垂直.其中的一条直线叫做另一条直线的_____,它们的交点叫做______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )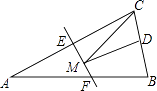
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以下现象中,属于平移的是( )
①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com