
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )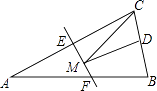
A.6
B.8
C.10
D.12
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3()
∴a∥b()
方法二::∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3()
又∠7=∠6()
∴∠3=∠6()
∴a∥b()
方法三::∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6()
∠4+∠6=180°(平角定义)
∴a∥b()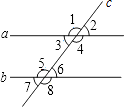
查看答案和解析>>
科目:初中数学 来源: 题型:
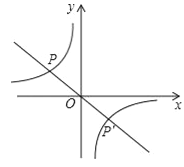
【题目】如图,点P(﹣3,1)是反比例函数![]() 的图象上的一点.
的图象上的一点.
(1)求该反比例函数的解析式;
(2)设直线y=kx与双曲线![]() 的两个交点分别为P和P′,当
的两个交点分别为P和P′,当![]() <kx时,直接写出x的取值范围.
<kx时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com