
����Ŀ���ڴ�����ȫ���������С��͡�ʡ�����������������У��������ˮ�����������ȹ���A��B������ˮ�����豸��20̨���Գ����ܱ���ˮ���д�������֪ÿ̨A���豸�۸�Ϊ12��Ԫ��ÿ̨B���豸�۸�Ϊ10��Ԫ��1̨A���豸��2̨B���豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A���豸��3̨B���豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2��Ҫ��ʹ��ˮ�����������豸���ʽ���230��Ԫ����ÿ�ܴ�����ˮ�����ֲ�����4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
���𰸡�
��1���⣺��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣���������
![]() ��
��
��� ![]() ��
��
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���⣺�蹺��A����ˮ�����豸x̨������B����ˮ�����豸��20��x��̨��
�� ![]() ��
��
���12.5��x��15��
��һ�ַ�������x=13ʱ��20��x=7�����ѵķ���Ϊ��13��12+7��10=226��Ԫ��
�ڶ��ַ�������x=14ʱ��20��x=6�����ѵķ���Ϊ��14��12+6��10=228��Ԫ��
�����ַ�������x=15ʱ��20��x=5�����ѵķ���Ϊ��15��12+5��10=230��Ԫ��
������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��
������������1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080�֣������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�����⣻
��2��������������г���Ӧ�IJ���ʽ�飬�Ӷ����Եõ��������Ӷ��������ÿ�ַ��������ʽ𣬴Ӷ����Խ���⣮
�����㾫����������Ŀ����֪����������һԪһ�β���ʽ���Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
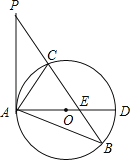
����Ŀ����ͼ����֪�ڡ�ABP�У�C��BP����һ�㣬��PAC=��PBA����O�ǡ�ABC�����Բ��AD�ǡ�O��ֱ�����ҽ�BP�ڵ�E��
��1����֤��PA�ǡ�O�����ߣ�
��2������C��CF��AD������Ϊ��F���ӳ�CF��AB�ڵ�G����AGAB=12����AC�ij���
��3�������㣨2���������£���AF��FD=1��2��GF=1�����O�İ뾶��sin��ACE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ���2�¡�����������Ρ�����ʦ������һ��˼���⣺
��ͼ����M��N�ֱ�����������ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q��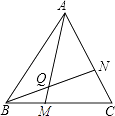
��1���жϡ�ABM���BCN�Ƿ�ȫ�ȣ���˵�����ɣ�
��2���жϡ�BQM�Ƿ�����60�㣬��˵�����ɣ�
��3���������еĵ�M��N�ֱ��ƶ���BC��CA���ӳ����ϣ���BM=CN���Ƿ��ܵõ���BQM=60�㣿��˵�����ɣ� 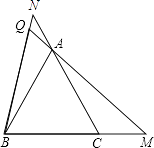
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ь��Ҫ��һ����Ь�����ǵ곤��Ӧ��ע�����ĸ�ͳ������������
A.ƽ����B.����C.����D.��λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���M����2��3���ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨��1��2017+���� ![]() ����3����2017��0�Ľ���ǣ� ��
����3����2017��0�Ľ���ǣ� ��
A.��10
B.��8
C.8
D.��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4�������16����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F�㣮����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬���CDM�ܳ�����СֵΪ�� ��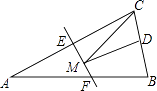
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
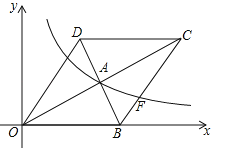
����Ŀ����10�֣���ͼ����ƽ��ֱ������ϵ�У�����OBCD�ı�OB��x���ϣ�����������![]() ��x��0����ͼ�����ζԽ��ߵĽ���A�������BC���ڵ�F����A������Ϊ��4��2����
��x��0����ͼ�����ζԽ��ߵĽ���A�������BC���ڵ�F����A������Ϊ��4��2����
��1�����������ı���ʽ��
��2�����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߶�CD�����߶�ABƽ�Ƶõ��ģ���A����2��5���Ķ�Ӧ��ΪC��3��7�������B����3��0���Ķ�Ӧ��D������Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com