
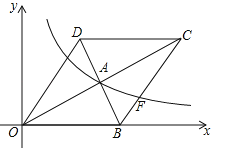
【题目】(10分)如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
【答案】(1)![]() ;(2)F(6,
;(2)F(6,![]() ).
).
【解析】
试题分析:(1)将点A的坐标代入到反比例函数的一般形式后求得k值即可确定函数的解析式;
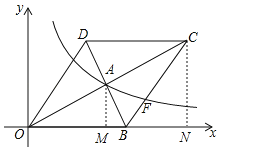
(2)过点A作AM⊥x轴于点M,过点C作CN⊥x轴于点N,首先求得点B的坐标,然后求得直线BC的解析式,求得直线和抛物线的交点坐标即可.
试题解析:(1)∵反比例函数![]() 的图象经过点A,A点的坐标为(4,2),∴k=2×4=8,∴反比例函数的解析式为
的图象经过点A,A点的坐标为(4,2),∴k=2×4=8,∴反比例函数的解析式为![]() ;
;
(2)过点A作AM⊥x轴于点M,过点C作CN⊥x轴于点N,由题意可知,CN=2AM=4,ON=2OM=8,∴点C的坐标为C(8,4),设OB=x,则BC=x,BN=8﹣x,在Rt△CNB中,![]() ,解得:x=5,∴点B的坐标为B(5,0),设直线BC的函数表达式为y=ax+b,直线BC过点B(5,0),C(8,4),∴
,解得:x=5,∴点B的坐标为B(5,0),设直线BC的函数表达式为y=ax+b,直线BC过点B(5,0),C(8,4),∴![]() ,解得:
,解得: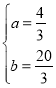 ,∴直线BC的解析式为
,∴直线BC的解析式为![]() ,根据题意得方程组
,根据题意得方程组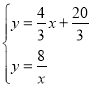 ,解此方程组得:
,解此方程组得:![]() 或
或![]() .∵点F在第一象限,∴点F的坐标为F(6,
.∵点F在第一象限,∴点F的坐标为F(6,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2 ![]() ,P是AC上的一个动点.
,P是AC上的一个动点.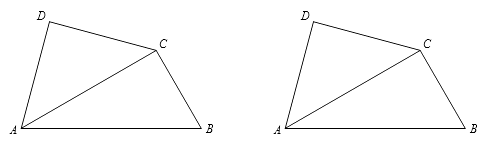
(1)当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时平行四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将方程x2-6x+3=0左边配成完全平方式,得到的方程是()
A. (x-3)2=-3 B. (x-3)2=6 C. (x-3)2=3 D. (x-3)2=12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分,全班40名同学参加了此次竞赛,他们的得分情况如下表所示
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
人数 | 2 | 5 | 13 | 10 | 7 | 3 |
则全班40名同学的成绩的中位数和众数分别是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于换季,一家服装店的老板想将某服装打折销售,于是她和正在上七年级的儿子商量打折方案,下面是她和儿子商量时的对话情景:
妈妈:“儿子,每件衣服按标价的5折出售,可以吗?”
儿子:“若每件衣服按标价的5折出售会亏本30元.”
妈妈:“那每件衣服按标价的8折出售呢?”
儿子:“若每件衣服按标价的8折出售将会赚60元.”
……
请根据上面的信息,解决问题:
(1)求这种服装的标价.
(2)若要不亏本,至少打几折?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com