
 如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°.
如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°. 分析 由角平分线的性质可得∠MOE=$\frac{1}{2}$∠MON=40°,结合AB⊥OM知∠1=90°-∠MOE=50°,继而根据“△ADB有两个相等的角”分①∠1=∠2=50°、②∠1=∠3=50°、③∠2=∠3三种情况分别求解可得答案.
解答 解:如图,
∵∠MON=80°,OE平分∠MON,
∴∠MOE=$\frac{1}{2}$∠MON=40°,
又∵AB⊥OM,
∴∠OAB=90°,
∴∠1=90°-∠MOE=50°,
①当∠1=∠2=50°时,∠OAC=∠OAB-∠2=40°;
②当∠1=∠3=50°时,∠2=180°-∠1-∠3=80°,
∴∠OAC=90°-∠2=10°;
③当∠2=∠3时,∵∠1=50°,
∴∠2=∠3=$\frac{180°-∠1}{2}$=65°,
∴∠OAC=∠OAB-∠2=25°;
综上,∠OAC的度数为10°、25°、40°,
故答案为:10°、25°、40°.
点评 本题主要考查角平分线的性质、垂直的定义、直角三角形的性质、三角形的内角和等知识点,根据角平分线的性质及直角三角形的性质得出△ADB一个内角度数是前提,分类讨论是解题的关键.


科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
对于有理数m,n,我们规定m n=mn-n,例如3
n=mn-n,例如3 5=3×5-5=10,则(-6)
5=3×5-5=10,则(-6) 4=________。
4=________。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
如图,点C在线段AB上,D是线段AC的中点。若CB=2,CD=3CB,则线段AB的长为( )

A. 6 B. 10 C. 14 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
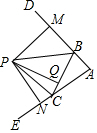 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )| A. | 一直不变 | B. | 一直减小 | C. | 一直增大 | D. | 先减小后增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com