
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5. 分析 先用垂径定理得出CD,进而用勾股定理求出AD,AC,再用已知角推导出∠FCE=∠AEC,即可得出FE=FC,进而判断出△FDE≌△FGE(ASA)即可得出DE=EG=$\frac{1}{2}$CE,再用角平分线定理求出CM,DM即可得出MH,进而利用勾股定理求出AM,再用△ADM∽△AED求出DE,最后用△DEC∽△AFC得出比例式即可求出AF.
解答 解:如图,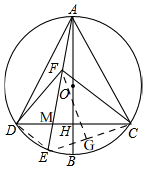 ∵AB是直径,CD是弦,AB⊥CD,
∵AB是直径,CD是弦,AB⊥CD,
∴DH=CH=$\frac{1}{2}$CD,
∵DC=AH,
∴AH=CD=2CH=2$\sqrt{37}$,
在Rt△ACH中,AD=AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{5}$CH=$\sqrt{185}$,
连接BE,CE,过点F作FG⊥CE,
∵AB是直径,CD是弦,AB⊥CD,
∴∠ADC=∠ACD,∠BAD=∠BAC=$\frac{1}{2}$∠CAD,
∵∠CFE=∠CAD,∠ADC=∠AEC,
∴∠ACD=∠FCE,
∵∠ADC=∠ACD,
∴∠FCE=∠AEC,
∴FE=FC,
∵FG⊥CE,
∴EG=CG=$\frac{1}{2}$EC,∠EFG=∠CFG=$\frac{1}{2}$∠EFC=$\frac{1}{2}$∠CAD=∠CAH,
∵∠DFE=∠CAH,
∴∠EFG=∠DEF,
∵∠AED=∠ACD=∠ADC=∠AEC,
在△FDE和△FGE中,$\left\{\begin{array}{l}{∠AED=∠AEC}\\{EF=EF}\\{∠DFE=∠EFG}\end{array}\right.$,
∴△FDE≌△FGE(ASA),
∴DE=EG=$\frac{1}{2}$CE,
∵∠AED=∠AEC,
∴$\frac{DE}{EC}=\frac{DM}{CM}=\frac{DE}{2DE}=\frac{1}{2}$,
∴CM=2DM,
∵CD=2CD=2$\sqrt{37}$=DM+CM=3DM,
∴DM=$\frac{2\sqrt{37}}{3}$,
CM=$\frac{4\sqrt{37}}{3}$,
∴MH=CM-CH=$\frac{\sqrt{37}}{3}$,
在Rt△AHM中,AM=$\sqrt{A{H}^{2}+M{H}^{2}}$=$\frac{37}{3}$,
∵∠ADM=∠AED,∠DAM=∠EAD,
∴△ADM∽△AED,
∴$\frac{DM}{DE}=\frac{AM}{AD}$,
∴$\frac{\frac{2\sqrt{37}}{3}}{DE}=\frac{\frac{37}{3}}{\sqrt{185}}$,
∴DE=2$\sqrt{5}$,
∵点A,D,E,C四点共圆,
∴∠DEC+∠CAD=180°,
∵∠CAD=∠EFC,
∴∠DEC+∠EFC=180°,
∵∠AFC+∠EFC=180°,
∴∠DEC=∠AFC,
∴∠CDE=∠CAF,
∴△DEC∽△AFC,
∴$\frac{DE}{AF}=\frac{CD}{AC}$,
∴AF=$\frac{DE•AC}{CD}=\frac{2\sqrt{5}×\sqrt{185}}{2\sqrt{37}}$=5.
故答案为5.
点评 此题是圆的综合题,主要考查了垂径定理,勾股定理,全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的判定和性质,角平分线定理等知识点;判断出FE=FC和CE=2DE是解本题的关键,求出DE是解本题的突破口;此题还可以拓展:如判断点O在CE的垂直平分线上,DF与DE垂直等.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为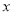 、小明掷B立方体朝上的数字为
、小明掷B立方体朝上的数字为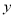 来确定点P(
来确定点P(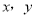 ),那么它们各掷一次所确定的点P落在已知抛物线
),那么它们各掷一次所确定的点P落在已知抛物线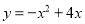 上的概率为( )
上的概率为( )
A. 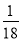 B.
B. 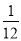 C.
C. 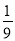 D.
D. 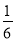
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
角度换算:45.6°=___________°___________'。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°.
如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
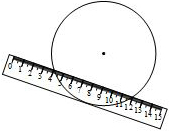 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
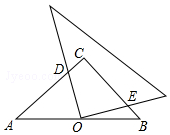 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com