
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
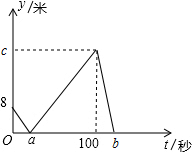 甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.
甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 绝对值等于其本身的有理数只有0,1 | |
| B. | 相反数等于其本身的有理数只有零 | |
| C. | 倒数等于其本身的有理数只有1 | |
| D. | 最小的数是零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
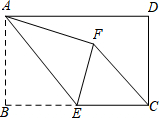 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠1=∠2,∠4=∠5,∠3=∠E,试说明AE∥BD,AD∥BC,请完成下列证明过程.
如图,已知∠1=∠2,∠4=∠5,∠3=∠E,试说明AE∥BD,AD∥BC,请完成下列证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com