
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在轴和轴上,其中OA=6,OC=3.已知反比例函数 (x>0)的图象经过BC边上的中点D,交AB于点E.
(x>0)的图象经过BC边上的中点D,交AB于点E.
(1)k的值为 ;
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.

(1)9;(2)S△OCD=S△OBE,理由见解析.
【解析】
试题分析:(1)根据题意得出点D的坐标,从而可得出k的值:
∵OA=6,OC=3,点D为BC的中点,∴D(3,3).
∵反比例函数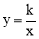 (x>0)的图象经过点D,∴k=3×3=9.
(x>0)的图象经过点D,∴k=3×3=9.
(2)根据三角形的面积公式和点D,E在函数的图象上,可得出S△OCD=S△OAE,再由点D为BC的中点,可得出S△OCD=S△OBD,即可得出结论.
试题解析:【解析】
(1)9.
(2)S△OCD=S△OBE,理由是:
∵点D,E在函数的图象上,∴S△OCD=S△OAE=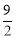 ,
,
∵点D为BC的中点,∴S△OCD=S△OBD,即S△OBE=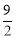 .
.
∴S△OCD=S△OBE.
考点:1.曲线上点的坐标与方程的关系;2.反比例函数系数k的几何意义;3.矩形的性质.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:解答题
已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
【解析】
因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为 .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:选择题
已知如图,一次函数y=ax+b和反比例函数 的图象相交于A、B两点,不等式ax+b>
的图象相交于A、B两点,不等式ax+b> 的解集为( )
的解集为( )

A.x<﹣3 B.﹣3<x<0或x>1 C.x<﹣3或x>1 D.﹣3<x<1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
2014年巴西世界杯足球赛正在如火如荼的进行,小明和喜爱足球的伙伴们一起预测“巴西队”能否获得本届杯赛的冠军,他们分别在3月、4月、5月、6月进行了四次预测,并且每次参加预测的人数相同,小明根据四次预测结果绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)每次有 人参加预测;
(2)计算6月份预测“巴西队”夺冠的人数;
(3)补全条形统计图和折线统计图.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:选择题
如图,A点的坐标为(﹣4,0),直线 与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为( )
与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com