
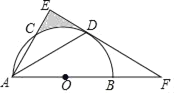
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
【答案】(1)证明见解析 (2)![]() ﹣6π
﹣6π
【解析】
(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;
(2)直接利用得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD,求出答案.
(1)证明:连接OD,
∵D为弧BC的中点,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∵DE⊥AC,
∴∠E=90°,
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF为半圆O的切线;
(2)解:连接OC与CD,
∵DA=DF,
∴∠BAD=∠F,
∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°,
∵OC=OA,
∴△AOC为等边三角形,
∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°,
∴∠DOF=60°,
在Rt△ODF中,DF=6![]() ,
,
∴OD=DFtan30°=6,
在Rt△AED中,DA=6![]() ,∠CAD=30°,
,∠CAD=30°,
∴DE=DAsin30°=3![]() ,EA=DAcos30°=9,
,EA=DAcos30°=9,
∵∠COD=180°﹣∠AOC﹣∠DOF=60°,
由CO=DO,
∴△COD是等边三角形,
∴∠OCD=60°,
∴∠DCO=∠AOC=60°,
∴CD∥AB,
故S△ACD=S△COD,
∴S阴影=S△AED﹣S扇形COD=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
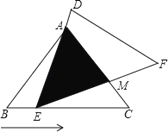
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由;
(3)求当线段AM最短时的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一扇门ABCD,宽度AB=1m,A到墙角E的距离AE=0.5m,设E,A,B在一条直线上,门打开后被与门所在墙面垂直的墙阻挡(EA⊥EB′),边BC靠在墙B'C'的位置.
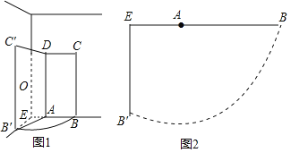
(1)求∠BAB'的度数;
(2)打开门后,门角上的点B在地面扫过的痕迹为弧BB',设弧BB'与两墙角线围成区域(如图2)的面积为S(m2),求S的值(π≈3.14,![]() ≈1.73,精确到0.1).
≈1.73,精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
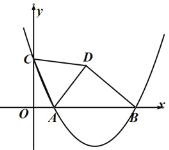
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
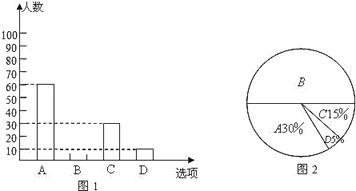
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A.1.5小时以上;B.1~1.5小时;C.0.5~1小时;D.0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在1小时以下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com