
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
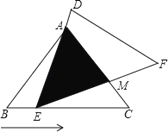
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由;
(3)求当线段AM最短时的长度
【答案】(1)证明见解析;(2)BE=1或![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证得∠CEM=∠BAE,则可证得:△ABE∽△ECM;
(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案;
(3)先设BE=x,由△ABE∽△ECM,根据相似三角形的对应边成比例,易得CM=-![]() (x-3)2+
(x-3)2+![]() ,利 用二次函数的性质,继而求得线段AM的最小值.
,利 用二次函数的性质,继而求得线段AM的最小值.
试题解析:(1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC-EC=6-5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴![]()
∴CE=![]()
∴BE=6-![]()
∴BE=1或![]()
(3)解:设BE=x,
又∵△ABE∽△ECM,
∴![]()
即:![]()
∴CM=![]()
∴AM=-5-CM=![]()
∴当x=3时,AM最短为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
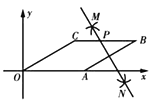
A.![]() B.
B.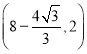 C.
C.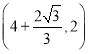 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
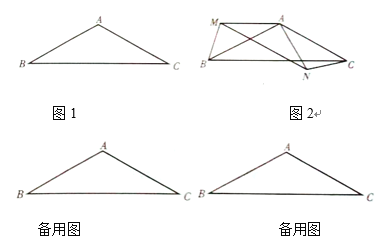
【题目】如图1,在![]() 中,
中,![]() ,
,![]() .
.
问题情境1:(1)![]() 与
与![]() 的数量关系为_______;
的数量关系为_______;
问题情境2:(2)如图2,若![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的数量关系是什么.请说明理由;
的数量关系是什么.请说明理由;
拓展延伸:(3)将图2中的![]() 绕点
绕点![]() 顺时针旋转角度
顺时针旋转角度![]() (
(![]() ),在旋转过程中,当
),在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在同一条直线上时,请直接写出
三点在同一条直线上时,请直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
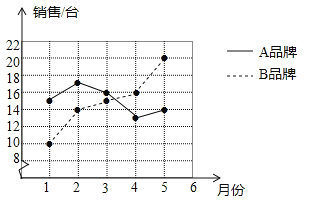
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
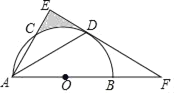
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com