
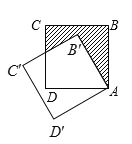
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB’C’D’,图中阴影部分的面积为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设B′C′与CD的交点为E,连接AE,利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积,列式计算即可得解.
如图,设B′C′与CD的交点为E,连接AE,
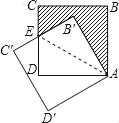
在Rt△AB′E和Rt△ADE中,
![]() ,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE=![]() ×60°=30°,
×60°=30°,
∴DE=1×![]() =
=![]() ,
,
∴阴影部分的面积=1×1﹣2×(![]() ×1×
×1×![]() )=1﹣
)=1﹣![]() .
.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)

(1)若某月小萱主叫通话时间为220分钟,上网流量为800 MB,则她按套餐1计费需 元,按套餐2计费需 元;若某月小花按套餐2计费需129元,主叫通话时间为240分钟,则上网流量为 MB.
(2)若上网流量为540 MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
(3)上网流量为540 MB,直接写出当月主叫通话时间t(分钟)满足什么条件时,选择套餐1省钱?当每月主叫通话时间t(分钟)满足什么条件时,选择套餐2省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图. 请根据图表信息解答下列问题:
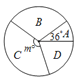
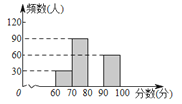
(1)扇形统计图中的m=___,并在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在____组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD的长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示5与
表示5与![]() 之差的绝对值,实际上也可以理解为5与
之差的绝对值,实际上也可以理解为5与![]() 两数在数轴上所对应的两点之间的距离.回答下列问题:
两数在数轴上所对应的两点之间的距离.回答下列问题:
(1)![]() _______.
_______.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() 成立,这样的整数是______.
成立,这样的整数是______.
(3)对于任何有理数![]() ,
,![]() 的最小值是______.
的最小值是______.
(4)对于任何有理数![]() ,
,![]() 的最小值是_____,此时
的最小值是_____,此时![]() 的值是______.
的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(2,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>2),连接BC,以线段BC为边在第四象限内作等边三角形△CBD连接DA并延长交y轴于点E.

(1)在点C的运动过程中,△OBC和△ABD全等吗?请说明理由;
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化请说明理由;
(3)探究当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线AB上一点,过O点作射线
为直线AB上一点,过O点作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边OM在射线OB上,另一边ON在直线AB的下方.
处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点![]() 按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.
按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.

(2)继续将图2中的三角板绕点![]() 按逆时针方向旋转至图3的位置,使得ON在
按逆时针方向旋转至图3的位置,使得ON在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1开始绕点O按![]() 每秒的速度逆时针旋转
每秒的速度逆时针旋转![]() 的过程中, 是否存在
的过程中, 是否存在![]() 所在直线平分
所在直线平分![]() 和
和![]() 中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间
中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间![]() ,若不存在,说明理由.
,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光服装厂接受生产一些某种型号的学生服的订单,已知每3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用750m长的这种布料生产学生服,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
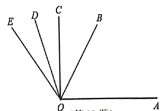
【题目】如图,已知:OB是∠AOE的平分线,OD是∠COE的平分线.
(1)若∠AOC= 90°,∠COE =30°,求∠BOD的度数;
(2)若(1)中的∠COE=α(α为锐角),其它条件不变,求∠BOD的度数;
(3)若(1)中的∠AOC=β,其它条件不变,求∠BOD的度数;
(4)从(1),(2),(3)的结果中猜想∠BOD与∠AOC的数量关系是________ ,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com