
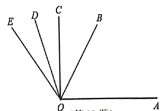
【题目】如图,已知:OB是∠AOE的平分线,OD是∠COE的平分线.
(1)若∠AOC= 90°,∠COE =30°,求∠BOD的度数;
(2)若(1)中的∠COE=α(α为锐角),其它条件不变,求∠BOD的度数;
(3)若(1)中的∠AOC=β,其它条件不变,求∠BOD的度数;
(4)从(1),(2),(3)的结果中猜想∠BOD与∠AOC的数量关系是________ ,并说明理由.
【答案】(1) 45°;(2) 45°;(3)![]() β;(4) ∠BOD=
β;(4) ∠BOD=![]() ∠AOC,理由见详解.
∠AOC,理由见详解.
【解析】
(1)求出∠AOE,根据角平分线定义得出∠BOE=![]() ∠AOE,∠DOE=
∠AOE,∠DOE=![]() ∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
(2)求出∠AOE,根据角平分线定义得出∠BOE=![]() ∠AOE,∠DOE=
∠AOE,∠DOE=![]() ∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
(3)求出∠AOE,根据角平分线定义得出∠BOE=![]() ∠AOE,∠DOE=
∠AOE,∠DOE=![]() ∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可;
(4)设∠AOC=α,∠COE=β,求出∠AOE,根据角平分线定义得出∠BOE=![]() ∠AOE,∠DOE=
∠AOE,∠DOE=![]() ∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可.
∠COE,代入求出∠BOE和∠DOE度数,根据∠BOD=∠BOE-∠DOE,代入求出即可.
(1)∵∠AOC=90°,∠COE=30°,
∴∠AOE=∠AOC+∠COE=120°,
∵OB是∠AOE的平分线,OD是∠COE的平分线,
∴∠BOE=![]() ∠AOE=60°,∠DOE=
∠AOE=60°,∠DOE=![]() ∠COE=15°,
∠COE=15°,
∴∠BOD=∠BOE∠DOE=60°15°=45°
(2)∵∠AOC=60°,∠COE=α,
∴∠AOE=∠AOC+∠COE=90°+α,
∵OB是∠AOE的平分线,OD是∠COE的平分线,
∴∠BOE=![]() ∠AOE=
∠AOE=![]() (90°+α),∠DOE=
(90°+α),∠DOE=![]() ∠COE=
∠COE=![]() α,
α,
∴∠BOD=∠BOE∠DOE=![]() (90°+α)
(90°+α)![]() α=45°
α=45°
(3)∵∠AOC=β,∠COE=30°,
∴∠AOE=∠AOC+∠COE=β+30°,
∵OB是∠AOE的平分线,OD是∠COE的平分线,
∴∠BOE=![]() ∠AOE=
∠AOE=![]() (β+30°),∠DOE=
(β+30°),∠DOE=![]() ∠COE=15°,
∠COE=15°,
∴∠BOD=∠BOE∠DOE= ![]() (β+30°) 15°=
(β+30°) 15°=![]() β.
β.
(4)∠BOD=![]() ∠AOC,
∠AOC,
理由是:设∠AOC=α,∠COE=β,
则∠AOE=∠AOC+∠COE=α+β,
∵OB是∠AOE的平分线,OD是∠COE的平分线,
∴∠BOE=![]() (α+β),∠DOE=
(α+β),∠DOE=![]() ∠COE=
∠COE=![]() β,
β,
∴∠BOD=∠BOE∠DOE= ![]() (α+β)
(α+β)![]() β=
β=![]() α,
α,
∵∠AOC=α,
∴∠BOD=![]() ∠AOC.
∠AOC.


科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.
在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算(-![]() )÷(
)÷(![]() -
-![]() )”.小明仔细思考了一番,用了一种不同的方法解决了这个问题:原式的倒数为(
)”.小明仔细思考了一番,用了一种不同的方法解决了这个问题:原式的倒数为(![]() -
-![]() )÷(-
)÷(-![]() )=(
)=(![]() -
-![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]() -
-![]() )=
)=![]() .
.
(1)请你通过计算验证小明的解法的正确性.
(2)由此可以得到结论:一个数的倒数的倒数等于_____.
(3)请你运用小明的解法计算:
(-![]() )÷(1
)÷(1![]() -
-![]() -
-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).

(1)AD= ,AB= ;
(2)∠BAD是直角吗?请说出理由;
(3)求点B到直线CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民消费价格指数是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.据统计,从2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率如下图所示:

根据上图提供的信息,下列推断中不合理的是( )
A.2018年12月的增长率为0.0%,说明与2018年11月相比,全国居民消费价格保持不变
B.2018年11月与2018年10月相比,全国居民消费价格降低0.3%
C.2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率中最小的是-0.4%
D.2019年1月到2019年8月,全国居民消费价格每月比上个月的增长率一直持续变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣13+28+62﹣77
(2)4﹣4+(﹣3)×(﹣![]() )
)
(3)﹣12006+[1﹣(2﹣22)×3]+12016
(4)(﹣6)×(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣8)
)×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负.某天自A地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2,-8,-12,-2,+12,+8,+5.
(1)问收工时距A地多远?
(2)若每千米路程耗油0.2升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com