
【题目】如图1,点![]() 为直线AB上一点,过O点作射线
为直线AB上一点,过O点作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边OM在射线OB上,另一边ON在直线AB的下方.
处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点![]() 按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.
按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.

(2)继续将图2中的三角板绕点![]() 按逆时针方向旋转至图3的位置,使得ON在
按逆时针方向旋转至图3的位置,使得ON在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1开始绕点O按![]() 每秒的速度逆时针旋转
每秒的速度逆时针旋转![]() 的过程中, 是否存在
的过程中, 是否存在![]() 所在直线平分
所在直线平分![]() 和
和![]() 中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间
中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间![]() ,若不存在,说明理由.
,若不存在,说明理由.

【答案】(1)90;(2)∠AOM∠NOC=30°,理由见解析;(3)存在,2秒或5秒或8秒.
【解析】
(1)根据旋转的性质可知,旋转角为∠MON;
(2)如图3,利用平角的定义,结合已知条件:∠AOC:∠BOC=1:2,求得∠AOC=60°,然后由直角的性质、图中角与角的数量关系推知∠AOM∠NOC=30°;
(3)需要分类讨论:当OM平分∠BOC时,旋转角是60°;当ON平分∠AOC时,旋转角为240°.
解:(1)根据旋转的性质可知:
旋转角为∠MON=90°.
故答案为:90.
(2)
如图3:∠AOM∠NOC=30°,理由如下:
∵∠AOC+∠BOC=180°,
∠AOC:∠BOC=1:2,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∴∠AON+∠CON=60°,①
∵∠MON=90°,
∴∠AOM+∠AON=90°,②
②①,得∠AOM∠CON=30°.
(3)
如图4,当OM平分∠BOC时,ON所在直线平分∠AOC,
∠BOM=60°,
∴三角板绕点O逆时针旋转60°,
此时t=60÷30=2(秒);
如图5,当ON平分∠AOC时,OM所在直线平分∠BOC,
∠CON=30°,
∴三角板绕点O逆时针旋转240°,
此时t=240÷30=8(秒).
当OM旋转150度时也符合要求,此时旋转了5秒.
答:旋转时间为2秒或5秒或8秒.


科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
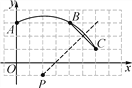
【题目】如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标,并求⊙P的半径(结果保留根号);
(2)判断点M(-1,1)与⊙P的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都华联商场经销甲、乙两种商品,甲种商品每件进价150元,售价200元;乙种商品每件进价350元,售价450元.
(1)该商场在“十一”黄金周期间销售甲、乙两种商品共100件,销售额为35000元,求甲、乙两种商品各销售了多少件?
(2)假若该商场在“十一”黄金周期间销售甲、乙两种商品进行如下优惠活动:
打折前一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元且不超过4000元 | 总售价打九折 |
超过4000元 | 总售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款2000元,第二天只购买乙种商品打折后一次性付款3240元,那么这两天他在该商场购买甲、乙两种商品一共多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b-2ab2+abc,小明错将“C=2A-B”看成“C=2A+B”,算得结果C=4a2b-3ab2+4abc.
(1)计算B的表达式;
(2)求C正确的结果的表达式;
(3)小芳说(2)中结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,求(2)中代数式的值.
,求(2)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.
在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣13+28+62﹣77
(2)4﹣4+(﹣3)×(﹣![]() )
)
(3)﹣12006+[1﹣(2﹣22)×3]+12016
(4)(﹣6)×(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣8)
)×(﹣8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com