
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】
(1)①首先证明△ABA1是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明△OCD1≌△OBA(AAS),推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题.
(1)证明:①如图1中,
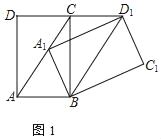
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
②如图2中,连接BD1.
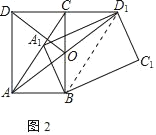
∵四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.
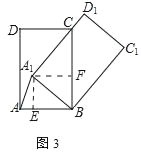
在Rt△A1BC中,∵∠CA1B=90°,BC=5.AB=3,
∴CA1=![]() =4,
=4,
∵![]() A1CA1B=
A1CA1B=![]() BCA1F,
BCA1F,
∴A1F=![]() ,
,
∵∠A1FB=∠A1EB=∠EBF=90°,
∴四边形A1EBF是矩形,
∴EB=A1F=![]() ,A1E=BF=
,A1E=BF=![]() ,
,
∴AE=3﹣![]() =
=![]() ,
,
在Rt△AA1E中,AA1=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,ADBC,E是AB 的中点,连接DE并延长交CB 的延长线于点F,点G在BC边上,且GDF ADF .
(1)求证:ADE ≌ BFE ;
(2)连接EG ,判断EG 与DF 的位置关系,并说明理由;
(3)若CDF 90,DF 4,CD 3 , CF 5 ,求RtCDF的三条角平分线的交点O 到边CF的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)

(1)若某月小萱主叫通话时间为220分钟,上网流量为800 MB,则她按套餐1计费需 元,按套餐2计费需 元;若某月小花按套餐2计费需129元,主叫通话时间为240分钟,则上网流量为 MB.
(2)若上网流量为540 MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
(3)上网流量为540 MB,直接写出当月主叫通话时间t(分钟)满足什么条件时,选择套餐1省钱?当每月主叫通话时间t(分钟)满足什么条件时,选择套餐2省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在纸面上有一数轴,如图所示,点O为原点,点A1、A2、A3、…分别表示有理数1、2、3、…,点B1、B2、B3、…分别表示有理数﹣1、﹣2、﹣3、….
![]()
(1)折叠纸面:
①若点A1与点B1重合,则点B2与点 重合;
②若点B1与点A2重合,则点A5与有理数 对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是 , ;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a﹣1|是表示点A到点 的距离;
②若|a﹣1|=3,则有理数a= ;
③若|a﹣1|+|a+2|=5,则有理数a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车沿着一条南北方向的公路来回行驶.某一天早晨从A地出发,晚上到达B地.约定向北为正,向南为负,当天记录如下:(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)问B地在A地何处,相距多少千米?
(2)若汽车行驶每千米耗油0.2升,那么这一天共耗油多少升?(精确到1升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边分别为a、b、c,则下列条件中不能判定△ABC是直角三角形的是( )
A. b2=a2﹣c2B. a:b:c=1:![]() :2
:2
C. ∠C=∠A﹣∠BD. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图. 请根据图表信息解答下列问题:
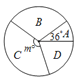
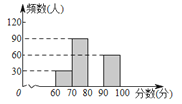
(1)扇形统计图中的m=___,并在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在____组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线AB上一点,过O点作射线
为直线AB上一点,过O点作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边OM在射线OB上,另一边ON在直线AB的下方.
处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点![]() 按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.
按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.

(2)继续将图2中的三角板绕点![]() 按逆时针方向旋转至图3的位置,使得ON在
按逆时针方向旋转至图3的位置,使得ON在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1开始绕点O按![]() 每秒的速度逆时针旋转
每秒的速度逆时针旋转![]() 的过程中, 是否存在
的过程中, 是否存在![]() 所在直线平分
所在直线平分![]() 和
和![]() 中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间
中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间![]() ,若不存在,说明理由.
,若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com