
【题目】如图,在四边形ABCD中,ADBC,E是AB 的中点,连接DE并延长交CB 的延长线于点F,点G在BC边上,且GDF ADF .
(1)求证:ADE ≌ BFE ;
(2)连接EG ,判断EG 与DF 的位置关系,并说明理由;
(3)若CDF 90,DF 4,CD 3 , CF 5 ,求RtCDF的三条角平分线的交点O 到边CF的距离.

【答案】(1)详见解析;(2)详见解析;(3)1.
【解析】
(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE;
(2)∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE=FE,即GE为底边上的中线,利用三线合一即可得到GE与DF垂直.
(3)根据直角三角形的内切圆的半径解答即可.
(1)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△ADE和△BFE中,
 ,
,
∴△ADE≌△BFE(AAS);

(2)EG与DF的位置关系是EG垂直平分DF,
理由为:连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,即GE为DF上的中线,
∴GE垂直平分DF.
(3)∵Rt△CDF的三条角平分线的交点O到边CF的距离即是△CDF的内切圆的半径,
∵∠CDF=90°,DF=4,CD=3,CF=5,
设△CDF的内切圆半径为r,
∵在Rt△CDF中,∠CDF=90°,DF=4,CD=3,CF=5,
∴S△CDF=![]() DCDF=
DCDF=![]() r(DF+DC+CF),
r(DF+DC+CF),
∴r=![]() =
=![]()
=1.
即Rt△CDF的三条角平分线的交点O到边CF的距离是1.


科目:初中数学 来源: 题型:
【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=![]()
![]() ,求⊙O半径的长.
,求⊙O半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
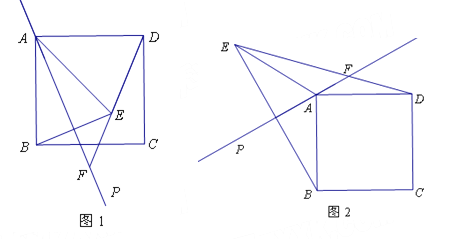
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若有理数a,b满足等式![]() ,则称a,b是“雉水有理数对”,记作
,则称a,b是“雉水有理数对”,记作![]() 如:数对
如:数对![]() ,
,![]() 都是“雉水有理数对”.
都是“雉水有理数对”.
![]() 数对
数对![]() ______
______![]() 填“是”或“不是”
填“是”或“不是”![]() “雉水有理数对”;
“雉水有理数对”;
![]() 若
若![]() 是“雉水有理数对”,求m的值;
是“雉水有理数对”,求m的值;
![]() 请写出一个符合条件的“锥水有理数对”______
请写出一个符合条件的“锥水有理数对”______![]() 注意:不能与题目中已有的“雉水有理数对”重复
注意:不能与题目中已有的“雉水有理数对”重复![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
(1)(获得结论)在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
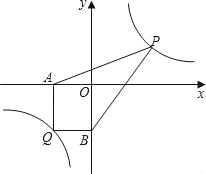
(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com