
����Ŀ�����Ķ����⣩����������ʵ��a��b��
��(![]() ��
��![]() )2��0��
)2��0��
��a��2![]() +b��0��
+b��0��
��a+b��2![]() ��(ֻ�е�a��bʱ��a+b����2
��(ֻ�е�a��bʱ��a+b����2![]() )��
)��
(1)����ý��ۣ���a+b��2![]() (a��b��Ϊ��ʵ��)�У���abΪ��ֵp��
(a��b��Ϊ��ʵ��)�У���abΪ��ֵp��
��a+b��2![]() ��ֻ�е�a��bʱ��a+b����Сֵ2
��ֻ�е�a��bʱ��a+b����Сֵ2![]() ��
��
�����������ݣ��ش��������⣺��m��0��ֻ�е�m���� ��ʱ��m+![]() ����Сֵ�� ����
����Сֵ�� ����
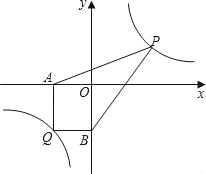
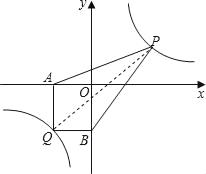
(2)��̽��Ӧ�ã���֪��Q(��3����4)��˫����y��![]() ��һ�㣬��Q��QA��x���ڵ�A����QB��y���ڵ�B����PΪ˫����y��
��һ�㣬��Q��QA��x���ڵ�A����QB��y���ڵ�B����PΪ˫����y��![]() (x��0)������һ�㣬����PA��PB�����ı���AQBP���������Сֵ��
(x��0)������һ�㣬����PA��PB�����ı���AQBP���������Сֵ��
���𰸡�(1)2��4��(2)24.
��������
��1�������IJ��Ͽɵã���m��![]() ʱ��m+
ʱ��m+![]() ȡ�����ֵ���ݴ˼�����⣻
ȡ�����ֵ���ݴ˼�����⣻
��2������PQ����P��x��![]() �������ݸ����ı���AQBP���������AQP�����+��QBP��������Ӷ�����x��ʾ���ı��ε�����������Ķ������н��ܵIJ���ʽ�����ʼ�����⣮
�������ݸ����ı���AQBP���������AQP�����+��QBP��������Ӷ�����x��ʾ���ı��ε�����������Ķ������н��ܵIJ���ʽ�����ʼ�����⣮
(1)��������õ�m��![]() ʱ��m��2����ʱm+
ʱ��m��2����ʱm+![]() ��4��
��4��
�ʴ��ǣ�2��4��
(2)����PQ����P(x��![]() )��
)��
��S�ı���AQBP��![]() ��4(x+3)+
��4(x+3)+![]() ��3(
��3(![]() +4)
+4)
��2x+![]() +12��12+12��24��
+12��12+12��24��
����СֵΪ24��


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij�ֽ�������Ҫ���в������պͶ�������������Ҫ�������յ�800����Ȼ��ֹͣ���ս��ж������������8minʱ�������¶Ƚ�Ϊ600��������ʱ�¶�y��������ʱ��x��min����һ�κ�����ϵ������ʱ���¶�y��������ʱ��x��min���ɷ�����������ϵ����ͼ������֪�ò��ϳ�ʼ�¶���32����

��1���ֱ�����������պͶ���ʱy��x�ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ��
��2�����ݹ���Ҫ�������¶ȵ���480��ʱ����ֹͣ��������ô����IJ���ʱ���ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
��1�������ϱ�ʾ4��1������֮��ľ����� ����ʾ-3��2����֮��ľ����� ��һ��أ������ϱ�ʾ��m����n������֮��ľ������|m-n|��
��2�����|x+1|=3����ôx= ��
��3����|a-3|=2��|b+2|=1������a��b�������ϱ�ʾ�����ֱ��ǵ�A����B����A��B �������������� ��
��4���������ϱ�ʾa�ĵ�λ��-4��2֮�䣬��|a+4|+|a-2= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���糿�ܲ��������Լ��ҳ�����������2km����С��ң�����������1.5km����С��ң�Ȼ������������4.5km����ѧУ����������ܻص��Լ��ң�
��1����С����Ϊԭ�㣬����Ϊ��������1����λ���ȱ�ʾ1km����ͼ�е������ϣ��ֱ��õ�A��ʾ��С��ң��õ�B��ʾ��С��ң��õ�C��ʾ��ѧУ��λ�ã�
![]()
��2����С�����ѧУ֮��ľ��룻
��3�����С���ܲ����ٶ���250m/min����ôС���ܲ�һ�����˶ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ȤС�鿪չ������ֽ��������۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչ��������һ���۵�ֽƬ��ʹ��A����EF�ϣ���ʹ�ۺ۾�����B���õ��ۺ�BM��ͬʱ�õ��߶�BN���۲�̽�����Եõ���NBC�Ķ����ǣ�������

A. 20��B. 25��C. 30��D. 35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
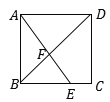
����Ŀ����ͼ��ʾ����������ABCD�У���E��BC����һ�㣬��BE:EC=2��1��AE��BD���ڵ�F�����AFD���ı���DFEC�����֮����________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ����Rt��ABC����A��90����AB��AC��A����2��0����
B��0��1����C��d��2����
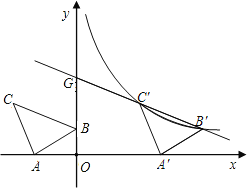
��1����d��ֵ��
��2������ABC��x���������ƽ�ƣ��ڵ�һ������B��C����Ķ�Ӧ��B����C����������ij����������ͼ
���ϡ��������������������ʹ�ʱ��ֱ��B��C���Ľ���ʽ��
��3���ڣ�2���������£�ֱ��B��C����y���ڵ�G�����Ƿ����x���ϵĵ�M�ͷ���������ͼ���ϵĵ�P��
ʹ���ı���PGMC����ƽ���ı��Ρ�������ڣ��������M�͵�P�����ꣻ��������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com