
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжагаRtЁїABCЃЌЁЯAЃН90ЁуЃЌABЃНACЃЌAЃЈЃ2ЃЌ0ЃЉЁЂ
BЃЈ0ЃЌ1ЃЉЁЂCЃЈdЃЌ2ЃЉЁЃ
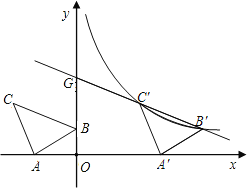
ЃЈ1ЃЉЧѓdЕФжЕЃЛ
ЃЈ2ЃЉНЋЁїABCбиxжсЕФе§ЗНЯђЦНвЦЃЌдкЕквЛЯѓЯоФкBЁЂCСНЕуЕФЖдгІЕуBЁфЁЂCЁфе§КУТфдкФГЗДБШР§КЏЪ§ЭМ
ЯёЩЯЁЃЧыЧѓГіетИіЗДБШР§КЏЪ§КЭДЫЪБЕФжБЯпBЁфCЁфЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБЯпBЁфCЁфНЛyжсгкЕуGЁЃЮЪЪЧЗёДцдкxжсЩЯЕФЕуMКЭЗДБШР§КЏЪ§ЭМЯёЩЯЕФЕуPЃЌ
ЪЙЕУЫФБпаЮPGMCЁфЪЧЦНааЫФБпаЮЁЃШчЙћДцдкЃЌЧыЧѓГіЕуMКЭЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЁОД№АИЁПЃЈ1ЃЉ-3ЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЈ3ЃЉPЁфЃЈ
ЃЈ3ЃЉPЁфЃЈ![]() ЃЌ5ЃЉЃЌMЁфЃЈ
ЃЌ5ЃЉЃЌMЁфЃЈ![]() ЃЌ0ЃЉЃЌдђЕуPЁфЮЊЫљЧѓЕФЕуPЃЌЕуMЁфЮЊЫљЧѓЕФЕуMЁЃ
ЃЌ0ЃЉЃЌдђЕуPЁфЮЊЫљЧѓЕФЕуPЃЌЕуMЁфЮЊЫљЧѓЕФЕуMЁЃ
ЁОНтЮіЁП
НтЃКЃЈ1ЃЉзїCNЁЭxжсгкЕуNЁЃ
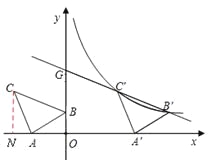
дкRtЁїCNAКЭRtЁїAOBжаЃЌ
ЁпNCЃНOAЃН2ЃЌACЃНAB
ЁрRtЁїCNAЁеRtЁїAOBЃЈHLЃЉЁЃ
ЁрANЃНBOЃН1ЃЌNOЃНNAЃЋAOЃН3ЃЌ
гжЁпЕуCдкЕкЖўЯѓЯоЃЌЁрdЃНЃ3ЁЃ
ЃЈ2ЃЉЩшЗДБШР§КЏЪ§ЮЊ![]() ЃЌЕуCЁфКЭBЁфдкИУБШР§КЏЪ§ЭМЯёЩЯЃЌ
ЃЌЕуCЁфКЭBЁфдкИУБШР§КЏЪ§ЭМЯёЩЯЃЌ
ЩшCЁфЃЈcЃЌ2ЃЉЃЌдђBЁфЃЈcЃЋ3ЃЌ1ЃЉЁЃ
АбЕуCЁфКЭЃТЁфЕФзјБъЗжБ№ДњШы![]() ЃЌЕУkЃН2 cЃЛkЃНcЃЋ3ЁЃ
ЃЌЕУkЃН2 cЃЛkЃНcЃЋ3ЁЃ
Ёр2 cЃНcЃЋ3ЃЌcЃН3ЃЌдђkЃН6ЁЃЁрЗДБШР§КЏЪ§НтЮіЪНЮЊ![]() ЁЃ
ЁЃ
ЕУЕуCЁфЃЈ3ЃЌ2ЃЉЃЛBЁфЃЈ6ЃЌ1ЃЉЁЃ
ЩшжБЯпCЁфBЁфЕФНтЮіЪНЮЊyЃНaxЃЋbЃЌАбCЁфЁЂBЁфСНЕузјБъДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ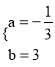 ЁЃ
ЁЃ
ЁржБЯпCЁфBЁфЕФНтЮіЪНЮЊ![]() ЁЃ
ЁЃ
ЃЈ3ЃЉЩшQЪЧG CЁфЕФжаЕуЃЌгЩGЃЈ0ЃЌ3ЃЉЃЌCЁфЃЈ3ЃЌ2ЃЉЃЌЕУЕуQЕФКсзјБъЮЊ![]() ЃЌЕуQЕФзнзјБъЮЊ
ЃЌЕуQЕФзнзјБъЮЊ
2ЃЋ![]() ЁЃЁрQЃЈ
ЁЃЁрQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЁЃ
ЃЉЁЃ
Й§ЕуQзїжБЯпlгыxжсНЛгкMЁфЕуЃЌ
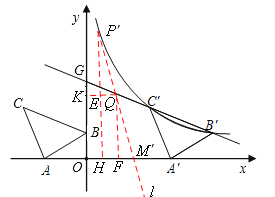
гы![]() ЕФЭМЯѓНЛгкPЁфЕуЃЌШєЫФБпаЮPЁфG MЁф CЁфЪЧЦНааЫФБпаЮЃЌдђгаPЁфQЃНQ MЁфЃЌвзжЊЕуMЁфЕФКсзјБъДѓгк
ЕФЭМЯѓНЛгкPЁфЕуЃЌШєЫФБпаЮPЁфG MЁф CЁфЪЧЦНааЫФБпаЮЃЌдђгаPЁфQЃНQ MЁфЃЌвзжЊЕуMЁфЕФКсзјБъДѓгк![]() ЃЌЕуPЁфЕФКсзјБъаЁгк
ЃЌЕуPЁфЕФКсзјБъаЁгк![]() ЁЃ
ЁЃ
зїPЁфЃШЁЭxжсгкЕуHЃЌQKЁЭyжсгкЕуKЃЌPЁфHгыQKНЛгкЕуEЃЌзїQFЁЭxжсгкЕуFЃЌ
дђЁїPЁфEQЁеЁїQFMЁф ЁЃ
ЩшEQЃНFMЁфЃНtЃЌдђЕуPЁфЕФКсзјБъxЮЊ![]() ЃЌЕуPЁфЕФзнзјБъyЮЊ
ЃЌЕуPЁфЕФзнзјБъyЮЊ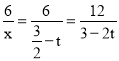 ЃЌ
ЃЌ
ЕуMЁфЕФзјБъЪЧЃЈ![]() ЃЌ0ЃЉЁЃ
ЃЌ0ЃЉЁЃ
ЁрPЁфEЃН![]() ЁЃ
ЁЃ
гЩPЁфQЃНQMЁфЃЌЕУPЁфE2ЃЋEQ2ЃНQF2ЃЋFMЁф2ЃЌЁр![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈОМьбщЃЌЫќЪЧЗжЪНЗНГЬЕФНтЃЉЁЃ
ЃЈОМьбщЃЌЫќЪЧЗжЪНЗНГЬЕФНтЃЉЁЃ
Ёр![]() ЃЌ
ЃЌ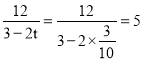 ЃЌ
ЃЌ![]() ЁЃ
ЁЃ
ЁрPЁфЃЈ![]() ЃЌ5ЃЉЃЌMЁфЃЈ
ЃЌ5ЃЉЃЌMЁфЃЈ![]() ЃЌ0ЃЉЃЌдђЕуPЁфЮЊЫљЧѓЕФЕуPЃЌЕуMЁфЮЊЫљЧѓЕФЕуMЁЃ
ЃЌ0ЃЉЃЌдђЕуPЁфЮЊЫљЧѓЕФЕуPЃЌЕуMЁфЮЊЫљЧѓЕФЕуMЁЃ
ЃЈ1ЃЉзїCNЁЭxжсгкЕуNЃЌгЩRtЁїCNAЁеRtЁїAOBМДПЩЧѓЕУdЕФжЕЁЃ
ЃЈ2ЃЉИљОнЦНвЦЕФаджЪЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓГіЗДБШР§КЏЪ§КЭжБЯпBЁфCЁфЕФНтЮіЪНЁЃ
ЃЈ3ЃЉИљОнЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌШЁG CЁфЕФжаЕуQЃЌЙ§ЕуQзїжБЯпlгыxжсНЛгкMЁфЕуЃЌгы![]() ЕФЭМЯѓНЛгкPЁфЕуЃЌЧѓГіPЁфQЃНQ MЁфЕФЕуMЁфКЭPЁфЕФзјБъМДПЩЁЃ
ЕФЭМЯѓНЛгкPЁфЕуЃЌЧѓГіPЁфQЃНQ MЁфЕФЕуMЁфКЭPЁфЕФзјБъМДПЩЁЃ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
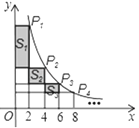
ЁОЬтФПЁПШчЭМЃЌдкКЏЪ§y=![]() (xЃО0)ЕФЭМЯѓЩЯгаЕуP1ЁЂP2ЁЂP3ЁЁЂPnЁЂPn+1ЃЌЕуP1ЕФКсзјБъЮЊ2ЃЌЧвКѓУцУПИіЕуЕФКсзјБъгыЫќЧАУцЯрСкЕуЕФКсзјБъЕФВюЖМЪЧ2ЃЌЙ§ЕуP1ЁЂP2ЁЂP3ЁЁЂPnЁЂPn+1ЗжБ№зїxжсЁЂyжсЕФДЙЯпЖЮЃЌЙЙГЩШєИЩИіОиаЮЃЌШчЭМЫљЪОЃЌНЋЭМжавѕгАВПЗжЕФУцЛ§ДгзѓжСгввРДЮМЧЮЊS1ЁЂS2ЁЂS3ЁЁЂSnЃЌдђSn=______ЃЎ(гУКЌnЕФДњЪ§ЪНБэЪО)
(xЃО0)ЕФЭМЯѓЩЯгаЕуP1ЁЂP2ЁЂP3ЁЁЂPnЁЂPn+1ЃЌЕуP1ЕФКсзјБъЮЊ2ЃЌЧвКѓУцУПИіЕуЕФКсзјБъгыЫќЧАУцЯрСкЕуЕФКсзјБъЕФВюЖМЪЧ2ЃЌЙ§ЕуP1ЁЂP2ЁЂP3ЁЁЂPnЁЂPn+1ЗжБ№зїxжсЁЂyжсЕФДЙЯпЖЮЃЌЙЙГЩШєИЩИіОиаЮЃЌШчЭМЫљЪОЃЌНЋЭМжавѕгАВПЗжЕФУцЛ§ДгзѓжСгввРДЮМЧЮЊS1ЁЂS2ЁЂS3ЁЁЂSnЃЌдђSn=______ЃЎ(гУКЌnЕФДњЪ§ЪНБэЪО)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФЯЙћРцЪЧЖЋББСЩФўЪЁЕФвЛДѓЬиВњЃЌЯжга20П№ФЯЙњРцЃЌвдУПП№25ЧЇПЫЮЊБъзМЃЌГЌЙ§ЛђВЛзуЕФЧЇПЫЪ§ЗжБ№гУе§ЁЂИКЪ§РДБэЪОЃЌМЧТМШчЯТЃК
гыБъзМжЪСПЕФВюжЕ ЃЈЕЅЮЛЃКЧЇПЫЃЉ | Ѓ3 | Ѓ2 | Ѓ1.5 | 0 | 1 | 2.5 |
П№Ъ§ | 1 | 4 | 2 | 3 | 2 | 8 |
ЃЈ1ЃЉ20П№ФЯЙћРцжаЃЌзюжиЕФвЛП№БШзюЧсЕФвЛП№жиЖрЩйЧЇПЫЃП
ЃЈ2ЃЉгыБъзМжиСПБШНЯЃЌ20П№ФЯЙћРцзмМЦГЌЙ§ЛђВЛзуЖрЩйЧЇПЫЃП
ЃЈ3ЃЉШєФЯЙћРцУПЧЇПЫЪлМл4дЊЃЌдђет20П№ПЩТєЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈдФЖСРэНтЃЉЖдгкШЮвте§ЪЕЪ§aЁЂbЃЌ
Ёп(![]() Љ
Љ![]() )2Ён0ЃЌ
)2Ён0ЃЌ
ЁрaЉ2![]() +bЁн0ЃЌ
+bЁн0ЃЌ
Ёрa+bЁн2![]() ЃЌ(жЛгаЕБaЃНbЪБЃЌa+bЕШгк2
ЃЌ(жЛгаЕБaЃНbЪБЃЌa+bЕШгк2![]() )ЃЎ
)ЃЎ
(1)ЃЈЛёЕУНсТлЃЉдкa+bЁн2![]() (aЁЂbОљЮЊе§ЪЕЪ§)жаЃЌШєabЮЊЖЈжЕpЃЌ
(aЁЂbОљЮЊе§ЪЕЪ§)жаЃЌШєabЮЊЖЈжЕpЃЌ
дђa+bЁн2![]() ЃЌжЛгаЕБaЃНbЪБЃЌa+bгазюаЁжЕ2
ЃЌжЛгаЕБaЃНbЪБЃЌa+bгазюаЁжЕ2![]() ЃЎ
ЃЎ
ИљОнЩЯЪіФкШнЃЌЛиД№ЯТСаЮЪЬтЃКШєmЃО0ЃЌжЛгаЕБmЃНЁЁ ЁЁЪБЃЌm+![]() газюаЁжЕЁЁ ЁЁЃЎ
газюаЁжЕЁЁ ЁЁЃЎ
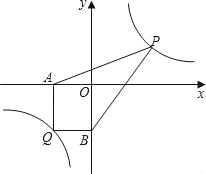
(2)ЃЈЬНЫїгІгУЃЉвбжЊЕуQ(Љ3ЃЌЉ4)ЪЧЫЋЧњЯпyЃН![]() ЩЯвЛЕуЃЌЙ§QзїQAЁЭxжсгкЕуAЃЌзїQBЁЭyжсгкЕуBЃЎЕуPЮЊЫЋЧњЯпyЃН
ЩЯвЛЕуЃЌЙ§QзїQAЁЭxжсгкЕуAЃЌзїQBЁЭyжсгкЕуBЃЎЕуPЮЊЫЋЧњЯпyЃН![]() (xЃО0)ЩЯШЮвтвЛЕуЃЌСЌНгPAЃЌPBЃЌЧѓЫФБпаЮAQBPЕФУцЛ§ЕФзюаЁжЕЃЎ
(xЃО0)ЩЯШЮвтвЛЕуЃЌСЌНгPAЃЌPBЃЌЧѓЫФБпаЮAQBPЕФУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊбХУРЗўзАГЇЯжгаAжжВМСЯ70УзЃЌBжжВМСЯ52УзЃЌЯжМЦЛЎгУетСНжжВМСЯЩњВњMЁЂNСНжжаЭКХЕФЪБзАЙВ80ЬзЃЎвбжЊзівЛЬзMаЭКХЕФЪБзАашгУAжжВМСЯ1.1УзЃЌBжжВМСЯ0.4УзЃЌПЩЛёРћ50дЊЃЛзівЛЬзNаЭКХЕФЪБзАашгУAжжВМСЯ0.6УзЃЌBжжВМСЯ0.9УзЃЌПЩЛёРћ45дЊЃЎЩшЩњВњMаЭКХЕФЪБзАЬзЪ§ЮЊxЃЌгУетХњВМСЯЩњВњСНжжаЭКХЕФЪБзАЫљЛёЕУЕФзмРћШѓЮЊyдЊЃЎ
ЃЈ1ЃЉЧѓyЃЈдЊЃЉгыxЃЈЬзЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБMаЭКХЕФЪБзАЮЊЖрЩйЬзЪБЃЌФмЪЙИУГЇЫљЛёРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцФкгаЁЯAOB=60ЁуЃЌЁЯAOC=40ЁуЃЌODЪЧЁЯAOBЕФЦНЗжЯпЃЌOEЪЧЁЯAOCЕФЦНЗжЯпЃЌЧѓЁЯDOEЕФЖШЪ§ЃЎ(ЧызїЭМНтД№)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
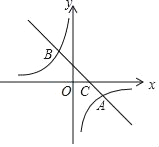
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y=k1x+bЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ4ЃЌЉ2ЃЉЁЂBЃЈЉ2ЃЌnЃЉСНЕуЃЌгыxжсНЛгкЕуCЃЎ
ЕФЭМЯѓНЛгкAЃЈ4ЃЌЉ2ЃЉЁЂBЃЈЉ2ЃЌnЃЉСНЕуЃЌгыxжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓk2ЃЌnЕФжЕЃЛ
ЃЈ2ЃЉЧыжБНгаДГіВЛЕШЪНk1x+b<![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉНЋxжсЯТЗНЕФЭМЯѓбиxжсЗелЃЌЕуAТфдкЕуAЁфДІЃЌСЌНгAЁфBЃЌAЁфCЃЌЧѓЁїAЁфBCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
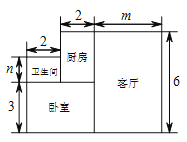
ЁОЬтФПЁПаЁЭѕЙКТђСЫвЛЬзвЛОгЪвЃЌЫћзМБИНЋЗПзгЕФЕиУцЦЬЩЯЕизЉЃЌЕиУцНсЙЙШчЭМЫљЪОЃЌИљОнЭМжаЫљИјЕФЪ§ОнЃЈЕЅЮЛЃКУзЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉгУКЌ ![]() ЕФДњЪ§ЪНБэЪОЕиУцЕФзмУцЛ§
ЕФДњЪ§ЪНБэЪОЕиУцЕФзмУцЛ§ ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉвбжЊ ![]() ЃЌЧвПЭЬќУцЛ§ЪЧЮРЩњМфУцЛ§ЕФ
ЃЌЧвПЭЬќУцЛ§ЪЧЮРЩњМфУцЛ§ЕФ ![]() БЖЃЌШчЙћЦЬ
БЖЃЌШчЙћЦЬ ![]() ЦНЗНУзЕизЉЕФЦНОљЗбгУЮЊ
ЦНЗНУзЕизЉЕФЦНОљЗбгУЮЊ ![]() дЊЃЌФЧУДаЁЭѕЦЬЕизЉЕФзмЗбгУЮЊЖрЩйдЊ?
дЊЃЌФЧУДаЁЭѕЦЬЕизЉЕФзмЗбгУЮЊЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇжјзїЁЖЫуЪѕбаОПЁЗвЛЪщжаЃЌЖдгкШЮвтЪЕЪ§ЃЌЭЈГЃгУx БэЪОВЛГЌЙ§ x ЕФзюДѓећЪ§ЃЌШч 3 ЃЌ 2 2 ЃЌ 2.1 3 ЁЃИјГіШчЯТНсТлЃКЂйx x ЃЛЂкШєx n ЃЌдђ x ЕФШЁжЕЗЖЮЇЪЧ n x n 1 ЃЛЂлЕБ1 x 1 ЪБЃЌ 1 x 1 x ЕФжЕЮЊ 1 Лђ 2ЃЛЂм x 2.75 ЪЧЗНГЬ 4x 2x 5 0 ЕФЮЈвЛвЛИіНтЁЃЦфжае§ШЗЕФНсТлгаЃЈ ЃЉ
A.ЂйЂкB.ЂкЂлC.ЂйЂлD.ЂлЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com