
【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
(1)求k2,n的值;
(2)请直接写出不等式k1x+b<![]() 的解集;
的解集;
(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC的面积.
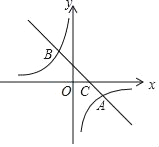
【答案】(1)k2=﹣8,n=4;(2)﹣2<x<0或x>4;(3)8
【解析】(1)将A点坐标代入y=![]() 求出k2=-8,得到反比例函数的解析式y=-
求出k2=-8,得到反比例函数的解析式y=-![]() ,再把B点坐标代入y=-
,再把B点坐标代入y=-![]() 得n=4;
得n=4;
(2)用函数的观点将不等式问题转化为函数图象问题;
(3)求出对称点坐标,求面积.
(1)将A(4,-2)代入y=![]() ,得k2=-8.
,得k2=-8.
∴y=-![]() ,
,
将(-2,n)代入y=-![]() ,得n=4.
,得n=4.
∴k2=-8,n=4
(2)根据函数图象可知:
-2<x<0或x>4
(3)将A(4,-2),B(-2,4)代入y=k1x+b,得k1=-1,b=2
∴一次函数的关系式为y=-x+2
与x轴交于点C(2,0)
∴图象沿x轴翻折后,得A′(4,2),
S△A'BC=(4+2)×(4+2)×![]() -
-![]() ×4×4-
×4×4-![]() ×2×2=8
×2×2=8
∴△A'BC的面积为8.


科目:初中数学 来源: 题型:
【题目】为了增强环境保护意识,![]() 月
月 ![]() 日“世界环境日”当天,若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市
日“世界环境日”当天,若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市 ![]() 个噪声测量点在某时刻的噪声声级(单位:
个噪声测量点在某时刻的噪声声级(单位:![]() ),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如表:
),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如表:
组 别 | 噪声声级分组 | 频 数 | 频 率 |
1 | 44.5--59.5 | 4 | 0.1 |
2 | 59.5--74.5 | a | 0.2 |
3 | 74.5--89.5 | 10 | 0.25 |
4 | 89.5--104.5 | b | c |
5 | 104.5--119.5 | 6 | 0.15 |
合 计 | 40 | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的 ![]() ,
,![]() ,
,![]() ;
;
(2)补全完整频数分布直方图(如图);

(3)从这个统计中,你认为噪声污染的噪音声级分布情况怎样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD,使AD和BC重合,得到折痕EF,把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN.观察探究可以得到∠NBC的度数是( )

A. 20°B. 25°C. 30°D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
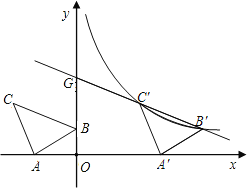
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、
B(0,1)、C(d,2)。
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图
像上。请求出这个反比例函数和此时的直线B′C′的解析式;
(3)在(2)的条件下,直线B′C′交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P,
使得四边形PGMC′是平行四边形。如果存在,请求出点M和点P的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=6,BC=8,点E、F分别是BC、CD边上的点,且AE⊥EF,BE=2,
(1)求证:AE=EF;
(2)延长EF交矩形∠BCD的外角平分线CP于点P(图2),试求AE与EP的数量关系;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果,并求出点P(x,y)落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得![]() .
.
(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com