
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

【答案】(1)解析式为y=x2﹣2x﹣3;(2)点P的坐标为(2![]() +1,4),(﹣2
+1,4),(﹣2![]() +1,4),(1,﹣4);(3)存在, Q点坐标为(1,﹣2).
+1,4),(1,﹣4);(3)存在, Q点坐标为(1,﹣2).
【解析】(1)∵抛物线y=x2+bx+c与![]() 轴的两个交点分别为A(-1,0),B(3,0)
轴的两个交点分别为A(-1,0),B(3,0)
∴![]() ┄ 2分
┄ 2分
解之,得![]() ┄ 3分
┄ 3分
∴所求抛物线的解析式为:y=x2-2x-3 ┄ 4分
(2)设点P的坐标为(x,y),由题意,得
S△ABC=![]() ×4×|y|=8 ┄ 5分
×4×|y|=8 ┄ 5分
∴|y|=4, ∴ y=±4 ┄ 6分
当y=4时, x2-2x-3=4 ∴ x1=1+![]() , x2=1-
, x2=1-![]() ┄ 7分
┄ 7分
当y=-4时,x2-2x-3=-4 ∴ x=1 ┄ 8分
∴当P点的坐标分别为![]() 、
、![]() 、(1,-4)时,S△PAB="8." ┄ 9分
、(1,-4)时,S△PAB="8." ┄ 9分
(3) 解法1: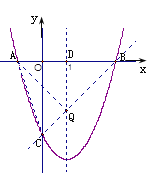
在抛物线y=x2-2x-3的对称轴上存在点Q, 使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小.
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点 ┄ 11分
设直线BC的解析式为y=kx-3.
∵直线BC过点B(3,0) ∴ 3k-3=0 ∴ k=1.
∴直线BC的解析式为 y=x-3 ┄ 12分
∴当x=1时,y=-2.
∴点Q的坐标为(1,-2). ┄ 13分
(3) 解法2:
在抛物线y=x2-2x-3的对称轴上存在点Q ,使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点. ┄ 11分
∵OC∥DQ,
∴ΔBDQ∽ΔBOC.
∴![]() ,即
,即![]() . ┄ 12分
. ┄ 12分
∴DQ=2. ∴点Q的坐标为(1,-2). ┄ 13分
(1)已知了抛物线过B、C两点,而抛物线的解析式中也只有两个待定系数,因此可将B、C的坐标代入抛物线的解析式中,即可求出待定系数的值,也就出了二次函数的解析式.
(2)根据(1)中得出的抛物线的解析式,可求得A点的坐标,也就能得出AB的长.△PAB中,AB的长为定值,那么可根据△PAB的面积求出P到AB的距离,即P点纵坐标的绝对值,然后将其代入抛物线的解析式中(分正负两个值)即可求出P点的坐标.
(3)本题的关键是找出Q点的位置,已知了B与A点关于抛物线的对称轴对称,因此只需连接BC,直线BC与对称轴的交点即为Q点.可根据B、C两点的坐标先求出直线BC的解析式,然后联立抛物线对称轴的解析式即可求出Q点的坐标.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C. “明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
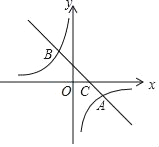
【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
(1)求k2,n的值;
(2)请直接写出不等式k1x+b<![]() 的解集;
的解集;
(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是随机抽取的某公司部分员工的月收入资料.
(1)请计算样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;并指出谁的推断比较科学合理,能直实地反映公司全体员工月收入水平。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 ![]() 的代数式表示地面的总面积
的代数式表示地面的总面积 ![]() ;
;
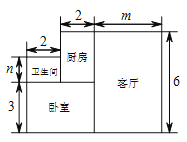
(2)已知 ![]() ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的 ![]() 倍,如果铺
倍,如果铺 ![]() 平方米地砖的平均费用为
平方米地砖的平均费用为 ![]() 元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
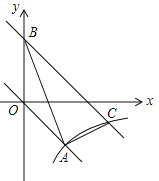
【题目】(2016四川省成都市)如图,在平面直角坐标xOy中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象都经过点A(2,﹣2).
的图象都经过点A(2,﹣2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式2x+4y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣2
)+(﹣2![]() )﹣(﹣32
)﹣(﹣32![]() )
)
(4)81.26﹣293.8+8.74+111
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com