
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
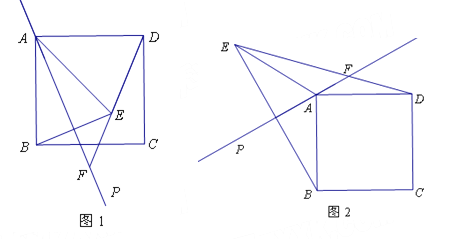
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
【答案】(1)①65,45;②![]() ;(2)2.
;(2)2.
【解析】试题分析:(1)①利用轴对称的性质以及等腰三角形的性质得出即可;②连接BD,BF先依据翻折的性质证明△BEF为等腰直角三角形,从而得到△BFD为直角三角形,由勾股定理可得到BF、FD、BD之间的关系,然后由△ABD为等腰直角三角形,从而得打BD与AB之间的关系,故此可得到BF、FD、AB之间的关系
(2)连接BF、DB.先依据翻折的性质和等腰三角形的性质证明∠BFD=90°,然后在△BDF中,由勾股定理可求得BD的长,从而求得AB的长,然后在等腰直角三角形EFB中可求得FG=GB=8,然后再Rt△AGB中,由勾股定理可求得AG的长,由AF=FG-AG可求得AG的长.
试题解析:(1)①翻折的性质可知:∠PAB=∠PAE=20°,AE=AB.
∴∠AEB=∠ABE=![]() ×(180°-40°)=70°.
×(180°-40°)=70°.
∵ABCD为正方形,
∴AB=AD,∠BAD=90°.
∴AE=AD,∠DAE=50°.
∴∠ADE=∠AED=![]() ×(180°-50°)=65°.
×(180°-50°)=65°.
∴∠BEF=180°-70°-65°=45°.
②线段AB、DF、EF之间的数量关系是:BF2+DF2=2AB2.
理由:连接BD,BF.
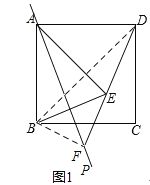
∵由翻折的性质可知:BF=FE,
∴∠FBE=∠FEB=45°.
∴∠BFE=90°.
∴BF2+DF2=DB2.
∵BD=![]() AB,
AB,
∴BD2=2AB2.
∴BF2+DF2=2AB2.
(2)如图2所示:连接BF、DB.

由翻折的性质可知:AB=AE,∠1=∠2,EF=BF=8![]() ,EG=GB.
,EG=GB.
又∵AD=AB,
∴AE=AD.
∴∠1=∠3.
∴∠2=∠3.
∵∠4=∠5,
∴∠5+∠3=∠2+∠4=90°.
∴△FDB和△EFB均为直角三角形,
∴BD=![]() .
.
∴AB=![]() BD=10
BD=10![]() ×
×![]() =10.
=10.
∵在Rt△EFB中,EF=BF,
∴EB=![]() EF=
EF=![]() ×8
×8![]() =16.
=16.
∴GF=EG=BG=8.
在Rt△ABG中,AG=![]() =6.
=6.
∴AF=FG-AG=8-6=2.


科目:初中数学 来源: 题型:
【题目】
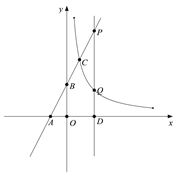
如图,在平面直角坐标系xoy中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线![]() 在第一象限内交于点C(1,m).
在第一象限内交于点C(1,m).
(1)求![]() 和
和![]() 的值;
的值;
(2)过![]() 轴上的点D(
轴上的点D(![]() ,0)作平行于y轴的直线
,0)作平行于y轴的直线![]() (
(![]() ),分别与直线AB和双曲线
),分别与直线AB和双曲线![]() 交于点P、Q,且PQ=2QD,求△APQ的面积.
交于点P、Q,且PQ=2QD,求△APQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种细胞开始有2个,1小时后分裂成4个并死去1个,2小时分裂成6个并死去1个,3小时后分裂成10个并死去1个,按此规律,5小时后细胞存活的个数是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com