
【题目】下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)

(1)若某月小萱主叫通话时间为220分钟,上网流量为800 MB,则她按套餐1计费需 元,按套餐2计费需 元;若某月小花按套餐2计费需129元,主叫通话时间为240分钟,则上网流量为 MB.
(2)若上网流量为540 MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
(3)上网流量为540 MB,直接写出当月主叫通话时间t(分钟)满足什么条件时,选择套餐1省钱?当每月主叫通话时间t(分钟)满足什么条件时,选择套餐2省钱?
【答案】(1)(1)143,109,900;(2)存在,若上网流量为540MB,当主叫通话时间为240分钟时,两种方式的计费相同,理由见解析;(3)当t<240时方式一省钱;当t>240时,方式二省钱
【解析】
(1)根据表中数据分别计算两种计费方式,第三空求上网流量时,可设上网流量为xMB,列方程求解即可;
(2)分0≤t<200时,当200≤t≤250时,当t>250时,三种情况分别计算讨论即可;
(3)本题结论可由(2)中结果直接得出.
解:(1)方式一:
49+0.2(220-200)+0.3(800-500)
=49+0.2×20+0.3×300
=49+4+90
143.
方式二:
69+0.2(800-600)
=69+0.2×200
=69+40
=109.
设上网流量为xMB,则
69+0.2(x-600)=129
解得x=900;
(2)当0≤t<200时,
49+0.3(540-500)=61≠69
∴此时不存在这样的t.
当200≤t≤250时,
49+0.2(t-200)+0.3(540-500)=69
解得t=240.
当t>250时,
49+0.2(t-200)+0.3(540-500)=69+0.15(t-250)
解得t=210(舍).
故若上网流量为540MB,当主叫通话时间为240分钟时,两种方式的计费相同.
(3)由(2)可知,当t<240时方式一省钱;当t>240时,方式二省钱.


科目:初中数学 来源: 题型:
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
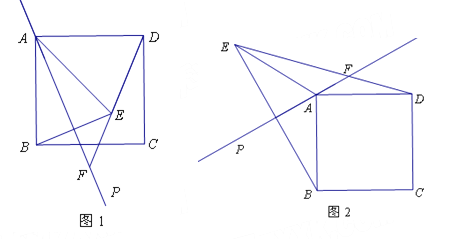
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
(1)(获得结论)在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
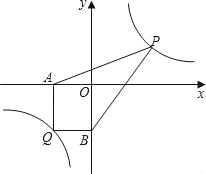
(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在数轴上表示的数分别为﹣12和8,两只蚂蚁M、N分别从A、B两点同时匀速出发,同向而行
时间/秒 | 0 | 1 | 5 |
A点位置 | ﹣12 | ﹣9 |
|
B点位置 | 8 |
| 18 |
(1)请填写表格;
(2)若两只蚂蚁在数轴上点P相遇,求点P在数轴上表示的数;
![]()
(3)若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
小敏进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为______;
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为______,取得最佳值最小值的数列为______(写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并完成题目
通过计算容易得到下列算式: ![]() ,
,![]() ,
,![]() ,...
,...
(1)填写计算结果![]() _ __,
_ __, ![]() _ __,
_ __, ![]() _ __,
_ __,
(2)观察以上各算式都是个位数字为5的数的平方数,可以看出规律,结果的末两位数字都是25,即是原来数字个位数字5的平方,前面的数字就是原来的数去掉5以后的数字乘以比它大1的结果,如: ![]() 就是
就是![]() 再连着写25得到225,
再连着写25得到225,![]() 就是
就是![]() 再连着写25得到625,
再连着写25得到625,![]() 就是
就是![]() 再连着写25得到1225,...
再连着写25得到1225,...
如果记-一个个位数字是5的多位数为![]() ,试用所学知识计算
,试用所学知识计算![]() 并归纳解释上述规律
并归纳解释上述规律
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com