
����Ŀ��С�����о���ѧ����ʱ����һ�����壺�������Ѿ��ź�˳������x1��x2��x3����Ϊ����x1��x2��x3������|x1|��![]() ��
��![]() ����������������Сֵ��Ϊ����x1��x2��x3�����ֵ�����磬��������2��-1��3����Ϊ|2|=2��
����������������Сֵ��Ϊ����x1��x2��x3�����ֵ�����磬��������2��-1��3����Ϊ|2|=2��![]() =
=![]() ��
��![]() =
=![]() ����������2��-1��3�����ֵΪ
����������2��-1��3�����ֵΪ![]() ��
��
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�����ֵ��������-1��2��3�����ֵΪ![]() ������3��-1��2�����ֵΪ1�����������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ
������3��-1��2�����ֵΪ1�����������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ![]() ���������ϲ��ϣ��ش��������⣺
���������ϲ��ϣ��ش��������⣺
��1������-4��-3��1�����ֵΪ______��
��2������-4��-3��2�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ______��ȡ�����ֵ��Сֵ������Ϊ______��д��һ�����ɣ���
��3����2��-9��a��a��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У�����Щ���е����ֵΪ1����a��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��2����4����2����3����4����3��4��
����3��2����4����2����3����4����3��4��
��������
��1�������������ϸ����ķ�����������Ӧ��ֵ���ɣ�
��2��������������ͬ��˳�����������ֵ���ɼ�����Կ�����Ҫ�����Щ���еļ�ֵ����Сֵ��ֻ�е�ǰ�������ĺ͵ľ���ֵ��С����Сֻ��Ϊ|��3+2|=1���ɴ˵ó��𰸼��ɣ�
��3������������Ӧ����ֵ�������������a����ֵ���ɣ�
��1����Ϊ|��4|=4��|![]() |=3.5��|
|=3.5��|![]() |=
|=![]() ���������Щ�4����3��2�ļ�ֵΪ
���������Щ�4����3��2�ļ�ֵΪ![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
��2�����еļ�ֵ����СֵΪ|![]() |=
|=![]() �����п���Ϊ����3��2����4����2����3����4���ʴ�Ϊ��
�����п���Ϊ����3��2����4����2����3����4���ʴ�Ϊ��![]() ����3��2����4����2����3����4��
����3��2����4����2����3����4��
��3������Щ���е����ֵ����1������
|![]() |=1����a=4��a=10��
|=1����a=4��a=10��
����a=10ʱ��![]() �������У�-9��a��2�����ֵΪ
�������У�-9��a��2�����ֵΪ![]() ��������������ȥ.
��������������ȥ.
�ʴ�Ϊ�� 4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�Ĵ�������������ö��ŷֿ�����
-8��0.275��![]() ��0����1.04��-��-3������
��0����1.04��-��-3������![]() ��|��2|.
��|��2|.
��1���������ϣ�{ ��}��
��2���������ϣ�{ ��}��
��3�����������ϣ�{ ��}��
��4���Ǹ������ϣ�{ ��}.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
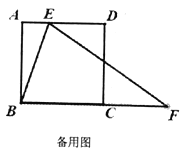
����Ŀ����ͼ��![]() ��������
��������![]() �ı�
�ı�![]() �ϵĶ��㣬
�ϵĶ��㣬![]() �DZ�
�DZ�![]() �ӳ����ϵ�һ�㣬��
�ӳ����ϵ�һ�㣬��![]() ��
��![]() ����
����![]() ��
��![]() .
.
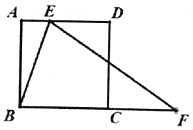
��1����![]() �ǵȱ�������ʱ����
�ǵȱ�������ʱ����![]() �ij���
�ij���
��2����![]() ��
��![]() �ĺ�������ʽ����д�����Ķ�����
�ĺ�������ʽ����д�����Ķ�����
��3����![]() ����ֱ��
����ֱ��![]() ���ۣ���
���ۣ���![]() ���ڵ�
���ڵ�![]() ������̽����
������̽����![]() �ܷ�Ϊ���������Σ�����ܣ������
�ܷ�Ϊ���������Σ�����ܣ������![]() �ij���������ܣ���˵������.
�ij���������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2016��Ϊ���á�����ƶ��,Ͷ���ʽ�1280��Ԫ������ذ��ã����滮Ͷ���ʽ��������ӣ�Ԥ��2018��Ͷ�˵��ʽ�2016���1600��Ԫ.
(1)��2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ���٣�
��2����2016����ذ��õľ���ʵʩ�У��õ�����Ͷ���ʽ���500��Ԫ�������Ȱ�Ǩ�ⷿ�������涨ǰ1000��������1000����ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬����2016��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±����й�����������4G�ײ����Ʒѷ�ʽ�����»����ѹ̶��գ����в���������ʱ�䣬����������������������ȡ������÷ѣ����г�ʱ���������������ּ��ճ�ʱ�Ѻͳ������ѣ�

(1)��ij��С������ͨ��ʱ��Ϊ220���ӣ���������Ϊ800 MB���������ײ�1�Ʒ��� Ԫ�����ײ�2�Ʒ��� Ԫ����ij��С�����ײ�2�Ʒ���129Ԫ������ͨ��ʱ��Ϊ240���ӣ�����������Ϊ MB��
(2)����������Ϊ540 MB���Ƿ����ij����ͨ��ʱ��t�����ӣ������ײ�1���ײ�2�ļƷ���ȣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
(3)��������Ϊ540 MB��ֱ��д����������ͨ��ʱ��t�����ӣ�����ʲô����ʱ��ѡ���ײ�1ʡǮ����ÿ������ͨ��ʱ��t�����ӣ�����ʲô����ʱ��ѡ���ײ�2ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ų����ε�ֽ���ۣ���ͼ��ʾ�ɵõ�һ���ۺۣ�ͼ�����ߣ����������ۣ�����ʱÿ���ۺ����ϴε��ۺ۱���ƽ�У������������κ��Ե�7���ۺۣ���ô�����Ĵο��Եõ� ���ۺۣ��������![]() �Σ����Եõ� ���ۺۣ�
�Σ����Եõ� ���ۺۣ�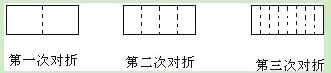
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������һ���ϱ�����Ĺ�·������ʻ.ijһ���糿��A�س��������ϵ���B��.Լ����Ϊ��������Ϊ���������¼���£�����λ��ǧ�ף�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��1����B����A�غδ���������ǧ�ף�
��2����������ʻÿǧ����0.2������ô��һ�칲���Ͷ�����������ȷ��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ʵ����У�ijУ�ס��ҡ�����λͬѧһͬ�����˸߷�ʱ�α����Ķ���·������·���Ļ�·�ij�����(ÿСʱͨ���۲�������������)����λ�㱨�߷�ʱ�εij�����������£�
��ͬѧ˵��������·������ΪÿСʱ10000��.��
��ͬѧ˵�����Ļ�·������·������ÿСʱ��2000��.��
��ͬѧ˵��������·��������3�����Ļ�·�������IJ��Ƕ���·��������2��.��
������������ṩ����Ϣ������߷�ʱ������·���Ļ�·�ij��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��2��0�������߶�OAΪ���ڵ������������ȱ���������AOB����CΪx��������һ���㣨OC��2��������BC�����߶�BCΪ���ڵ������������ȱ���������CBD����DA���ӳ���y���ڵ�E��

��1���ڵ�C���˶������У���OBC����ABDȫ������˵�����ɣ�
��2���ڵ�C���˶������У���CAD�Ķ����Ƿ��仯��������䣬�������CAD�Ķ���������仯��˵�����ɣ�
��3��̽������C�˶���ʲôλ��ʱ����A��E��CΪ������������ǵ��������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com