
����Ŀ�������ʵ����У�ijУ�ס��ҡ�����λͬѧһͬ�����˸߷�ʱ�α����Ķ���·������·���Ļ�·�ij�����(ÿСʱͨ���۲�������������)����λ�㱨�߷�ʱ�εij�����������£�
��ͬѧ˵��������·������ΪÿСʱ10000��.��
��ͬѧ˵�����Ļ�·������·������ÿСʱ��2000��.��
��ͬѧ˵��������·��������3�����Ļ�·�������IJ��Ƕ���·��������2��.��
������������ṩ����Ϣ������߷�ʱ������·���Ļ�·�ij��������Ƕ��٣�
���𰸡��߷�ʱ������·������ΪÿСʱ11000�����Ļ�·������ΪÿСʱ13000��.
������������������������·������ÿСʱx�����Ļ�·������ΪÿСʱy����Ȼ��������Ļ�·������·������ÿСʱ��2000�����͡�����·��������3�����Ļ�·�������IJ��Ƕ���·��������2���������г����������ⷽ����Ϳ����������·���Ļ�·�ij�������
�������߷�ʱ������·������ΪÿСʱx�����Ļ�·������ΪÿСʱy������������ã�
![]()
��ã�![]() ��
��
�𣺸߷�ʱ������·������ΪÿСʱ11000�����Ļ�·������ΪÿСʱ13000����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶��ѧ��ȤС�飬�ڹ㳡�ϲ���λ�����������ij������AC�ĸ߶ȣ���ͼ��ʾ�������ڵ�B��øý����ﶥ��A������Ϊ30����Ȼ������������ǰ��62�ף�����D�㣬�ٲ�øý����ﶥ��A������Ϊ60�㣨B��C��D������ͬһˮƽ���ϣ��Ҳ����ǵĸ߶Ⱥ��Բ��ƣ�����ý�����AC�ĸ߶ȣ������ȷ��1�ף��ο���ֵ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����о���ѧ����ʱ����һ�����壺�������Ѿ��ź�˳������x1��x2��x3����Ϊ����x1��x2��x3������|x1|��![]() ��
��![]() ����������������Сֵ��Ϊ����x1��x2��x3�����ֵ�����磬��������2��-1��3����Ϊ|2|=2��
����������������Сֵ��Ϊ����x1��x2��x3�����ֵ�����磬��������2��-1��3����Ϊ|2|=2��![]() =
=![]() ��
��![]() =
=![]() ����������2��-1��3�����ֵΪ
����������2��-1��3�����ֵΪ![]() ��
��
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�����ֵ��������-1��2��3�����ֵΪ![]() ������3��-1��2�����ֵΪ1�����������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ
������3��-1��2�����ֵΪ1�����������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ![]() ���������ϲ��ϣ��ش��������⣺
���������ϲ��ϣ��ش��������⣺
��1������-4��-3��1�����ֵΪ______��
��2������-4��-3��2�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ______��ȡ�����ֵ��Сֵ������Ϊ______��д��һ�����ɣ���
��3����2��-9��a��a��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У�����Щ���е����ֵΪ1����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ҫ�������ͼ��������
��ͼ����֪��A���߶�BC.
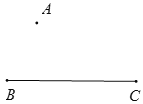
(1)����AB��
(2)������CA��
(3)�ӳ�BC����D��ʹ��BD=2BC��
(4)ͨ�������ɵá�ACD�Ķ����� ;
(5)����ACD��ƽ����CE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ��������Ŀ
ͨ���������õ�������ʽ: ![]() ��
��![]() ��
��![]() ��...
��...
��1���������![]() _ __,
_ __, ![]() _ __,
_ __, ![]() _ __��
_ __��
��2���۲����ϸ���ʽ���Ǹ�λ����Ϊ5������ƽ���������Կ������ɣ������ĩ��λ���ֶ���25������ԭ�����ָ�λ����5��ƽ����ǰ������־���ԭ������ȥ��5�Ժ�����ֳ��Ա�����1�Ľ������: ![]() ����
����![]() ������д25�õ�225��
������д25�õ�225��![]() ����
����![]() ������д25�õ�625��
������д25�õ�625��![]() ����
����![]() ������д25�õ�1225��...
������д25�õ�1225��...
�����-һ����λ������5�Ķ�λ��Ϊ![]() ,������ѧ֪ʶ����
,������ѧ֪ʶ����![]() �����ɽ�����������
�����ɽ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣���ͼ��ֱ��l������A��1��6���͵�B����3����2����

��1����ֱ��l�Ľ���ʽ��ֱ����������Ľ������ꣻ
��2�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У���BAD����BCD��ƽ���߷ֱ�BC��AD�ڵ�F��E.
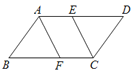
(1)��֤���ı���AFCE��ƽ���ı�����
(2)��BF=4��FC=3������ABCD���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ���
���![]() ��ƽ���ı���
��ƽ���ı���![]() ���ϵĶ��㣬��
���ϵĶ��㣬��![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶȣ��ӵ�
����λ���ȵ��ٶȣ��ӵ�![]() �˶�����
�˶�����![]() ����
����![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶȴӵ�
����λ���ȵ��ٶȴӵ�![]() ����
����![]() ����
����![]() �˶�.������һ���㵽���յ�ʱ����һ����ֹ֮ͣ�˶�.��
�˶�.������һ���㵽���յ�ʱ����һ����ֹ֮ͣ�˶�.��![]() ���
���![]() ͬʱ���������˶�ʱ��Ϊ
ͬʱ���������˶�ʱ��Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() .
.
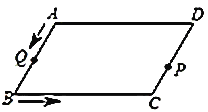
(1)��![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(2)![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ������һ��Ϊ�ᷭ�ۣ�����ǰ�����������������ɵ��ı���Ϊ����.
������һ��Ϊ�ᷭ�ۣ�����ǰ�����������������ɵ��ı���Ϊ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��6��ͬѧ�μ�һ��֪ʶ����������20���⣬ÿ���ֵ��ͬ����Ե÷֣������۷֣�������ǰ5��ͬѧ�ĵ÷���������±�����

��1�����е�m = ��n = ��
��2����С���6��ͬѧ˵�������֪ʶ�����ҵ���0��������������˵���Ƿ���ȷ�������ȷ���������λͬѧ����˶����⣻�������ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com