
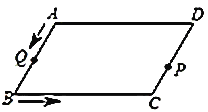
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 是平行四边形
是平行四边形![]() 边上的动点,点
边上的动点,点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 运动到点
运动到点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() →点
→点![]() →点
→点![]() 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点![]() 与点
与点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,将
为何值时,将![]() 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
【答案】(1)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;(2)
;(2)![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形. 当
不是等腰三角形,所以不存在符合条件的菱形. 当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
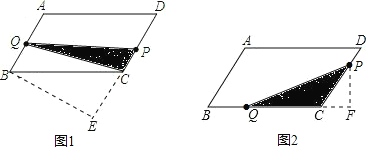
(1)当0<t≤2时,如图1,过点B作BE⊥CD,交DC的延长线于点E,根据三角形面积公式求得S关于t的函数关系式,当2<t≤4时,如图2,CP=t,BQ=2t-4,过点P作PF⊥BC,交BC的延长线于F点,由三角形面积公式求得S关于t的函数关系式,
(2)要使翻折前后的两个三角形所组成的四边形为菱形,则△CPQ为等腰三角形,则要CQ=CP,看看t是否存在.
(1)①当![]() 时,如图1,过点
时,如图1,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∴∠BED=90°,即∠BCE+∠CBE=90°,
∵四边形![]() 是平行四边形,∴AD∥BC,
是平行四边形,∴AD∥BC,
![]()
![]() ,
,![]()
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∵![]() ,
,
∴![]() ;
;
②当![]() 时,由题意得:CP=t,
时,由题意得:CP=t,![]() ,
,![]() ,
,
如图2,过点P作PF⊥BC,交BC的延长线于点F,
∴∠F=90°,
∵四边形![]() 是平行四边形,∴AB∥DC,
是平行四边形,∴AB∥DC,
∴![]() ,∵
,∵![]() ,
,
![]()
![]() ,
,
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() .
.
∴S=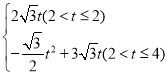 .
.
(2)当![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形.
不是等腰三角形,所以不存在符合条件的菱形.
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]()
![]() 当
当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
即为![]() 的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.
的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.


科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投人资金1280万元用于异地安置,并规划投入资金逐年增加,预计2018年投人的资金将比2016年多1600万元.
(1)从2016年到2018年,该地投人异地安置资金的年平均增长率为多少?
(2)在2016年异地安置的具体实施中,该地另外投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,试求2016年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆.”
乙同学说:“四环路比三环路车流量每小时多2000辆.”
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍.”
请你根据他们提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
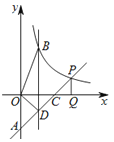
【题目】直线y=x-2与两坐标轴分别交于点A,C,交y=![]() (x>0) 于点P,PQ⊥x轴于点Q,CQ=1.
(x>0) 于点P,PQ⊥x轴于点Q,CQ=1.
(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x-2,y=![]() (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD的长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:P= ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
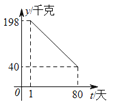
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(2,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>2),连接BC,以线段BC为边在第四象限内作等边三角形△CBD连接DA并延长交y轴于点E.

(1)在点C的运动过程中,△OBC和△ABD全等吗?请说明理由;
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化请说明理由;
(3)探究当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着出行方式的多样化,我市三类打车方式的收费标准如下:
出租车 | 滴滴快车 | 同城快车 |
3千米以内:8元 | 路程:1.4元/千米 | 路程:1.8元/千米 |
超过3千米的部分:2.4元/千米 | 时间:0.6元/分钟 | 时间:0.4元/分钟 |
如:假设打车的平均车速为40千米/小时,乘坐8千米,耗时8÷40×60=12分钟,出租车的收费为:8+2.4×(8﹣3)=20(元);滴滴快车的收费为:8×1.4+12×0.6=18.4(元);同城快车的收费为:8×1.8+12×0.4=19.2(元)
解决问题:
(1)小明乘车从高邮文体公园去盂城驿,全程10千米,如果小明使用滴滴快车,需要支付的打车费用为 元;
(2)小丽乘车从甲地去乙地,用滴滴快车比乘坐出租车节省了28.8元,求甲、乙两地的距离;
(3)同城快车为了和滴滴快车竞争客户,分别推出了优惠方式:滴滴快车对于乘车路程在5千米以上(含5千米)的客户每次收费立减11元;同城快车车费对折优惠.通过计算,对同城快车和滴滴快车两种打车方式,采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=BC=CD=DA,∠BAD=∠ABC=∠BCD=∠ADC=90°,E、F为BC、CD边上的点,若∠FAE=45°,试探究线段BE、EF、DF之间的数量关系,并说明理由.
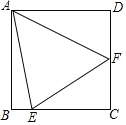
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com