
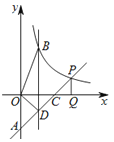
【题目】直线y=x-2与两坐标轴分别交于点A,C,交y=![]() (x>0) 于点P,PQ⊥x轴于点Q,CQ=1.
(x>0) 于点P,PQ⊥x轴于点Q,CQ=1.
(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x-2,y=![]() (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
【答案】(1)y=![]() ;(2)m=1.
;(2)m=1.
【解析】分析:(1)在y=x-2中,令y=0,解出x.得到C的坐标.设点P坐标为(a,a-2),得到QC=a-2.由S△CPQ=0.5,解方程得到a的值,从而得到P的坐标,即可得到结论.
(2)设B坐标为(m,![]() ),则D坐标为(m,m-2).,得到BD=
),则D坐标为(m,m-2).,得到BD=![]() -m+2.由S△BOD=2,解方程即可得到m的值.
-m+2.由S△BOD=2,解方程即可得到m的值.
详解:(1)在y=x-2中,当y=0时,x=2.∴C(2,0).
∵点P在y=x-2上,设点P坐标为(a,a-2),则Q(a,0),QC=a-2.
∵S△CPQ=0.5,∴![]() (a-2)(a-2)=0.5.
(a-2)(a-2)=0.5.
∵a>0,∴a=3,∴P(3,1).
∵点P在y=![]() (x>0)上,∴k=3,∴反比例函数解析式为:y=
(x>0)上,∴k=3,∴反比例函数解析式为:y=![]() ;
;
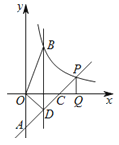
(2)由题意可得点B坐标为(m,![]() ),点D坐标为(m,m-2),∴BD=
),点D坐标为(m,m-2),∴BD=![]() -m+2.
-m+2.
∵S△BOD=2,∴ ![]() (
(![]() -m+2)m=2.
-m+2)m=2.
解得:m=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】学习有理数得乘法后,老师给同学们这样一道题目:
计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
聪聪:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
明明:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:29![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照下列要求完成作图及问题解答:
如图,已知点A和线段BC.
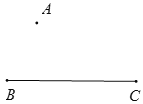
(1)连接AB;
(2)作射线CA;
(3)延长BC至点D,使得BD=2BC;
(4)通过测量可得∠ACD的度数是 ;
(5)画∠ACD的平分线CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,∠BAD,∠BCD的平分线分别交BC,AD于点F,E.
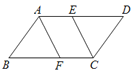
(1)求证:四边形AFCE是平行四边形;
(2)若BF=4,FC=3,求□ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 是平行四边形
是平行四边形![]() 边上的动点,点
边上的动点,点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 运动到点
运动到点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() →点
→点![]() →点
→点![]() 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点![]() 与点
与点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
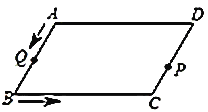
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,将
为何值时,将![]() 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.试猜想EF、BE、CF之间有怎样的关系,并说明理由.


(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,则刚才的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com