
【题目】某中学九年级数学兴趣小组,在广场上测量位于正东方向的某建筑物AC的高度,如图所示,他先在点B测得该建筑物顶点A的仰角为30°,然后向正东方向前行62米,到达D点,再测得该建筑物顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求该建筑物AC的高度(结果精确的1米,参考数值:![]() )
)

科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的大括号里(将各数用逗号分开):
-8,0.275,![]() ,0,-1.04,-(-3),-
,0,-1.04,-(-3),-![]() ,|-2|.
,|-2|.
(1)正数集合:{ …};
(2)分数集合:{ …};
(3)负整数集合:{ …};
(4)非负数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.
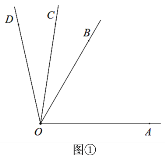
(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
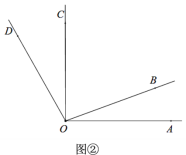
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 上的动点,
上的动点,![]() 是边
是边![]() 延长线上的一点,且
延长线上的一点,且![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
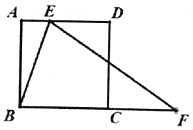
(1)当![]() 是等边三角形时,求
是等边三角形时,求![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
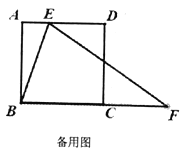
(3)把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,试探索:
处,试探索:![]() 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投人资金1280万元用于异地安置,并规划投入资金逐年增加,预计2018年投人的资金将比2016年多1600万元.
(1)从2016年到2018年,该地投人异地安置资金的年平均增长率为多少?
(2)在2016年异地安置的具体实施中,该地另外投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,试求2016年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆.”
乙同学说:“四环路比三环路车流量每小时多2000辆.”
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍.”
请你根据他们提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com