
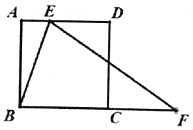
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 上的动点,
上的动点,![]() 是边
是边![]() 延长线上的一点,且
延长线上的一点,且![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)当![]() 是等边三角形时,求
是等边三角形时,求![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(3)把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,试探索:
处,试探索:![]() 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)当△BEF是等边三角形时,有∠ABE=∠ABC-∠EBC=90°-60°=30°,则可解Rt△ABE,求得BF即BE的长.
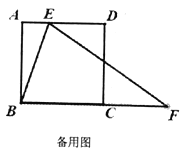
(2)作EG⊥BF,垂足为点G,则四边形AEGB是矩形,在Rt△EGF中,由勾股定理知,EF2=(BF-BG)2+EG2.即y2=(y-x)2+122.故可求得y与x的关系.
(3)当把△ABE沿着直线BE翻折,点A落在点A'处,应有∠BA'F=∠BA'E=∠A=90°,若△A'BF成为等腰三角形,必须使A'B=A'F=AB=12,有FA′=EF-A′E=y-x=12,故可由(2)得到的y与x的关系式建立方程组求得AE的值.
解:(1)当![]() 是等边三角形时,
是等边三角形时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)作![]() ,垂足为点
,垂足为点![]() ,
,
根据题意,得![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∴所求的函数解析式为![]() ;
;
(3)∵![]() ,
,
∴点![]() 落在
落在![]() 上,
上,
∴![]() ,
,![]() ,
,
∴要使![]() 成为等腰三角形,必须使
成为等腰三角形,必须使![]() .
.
而![]() ,
,![]() ,
,
∴![]() ,由(2)关系式可得:
,由(2)关系式可得:![]() ,
,
整理得![]() ,
,
解得![]() ,
,
经检验:![]() 都原方程的根,
都原方程的根,
但![]() 不符合题意,舍去,
不符合题意,舍去,
所以当![]() 时,
时,![]() 为等要三角形.
为等要三角形.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
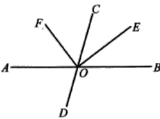
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,.
,.
(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求![]() 的度数;
的度数;
(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组,在广场上测量位于正东方向的某建筑物AC的高度,如图所示,他先在点B测得该建筑物顶点A的仰角为30°,然后向正东方向前行62米,到达D点,再测得该建筑物顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求该建筑物AC的高度(结果精确的1米,参考数值:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
(1)(获得结论)在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
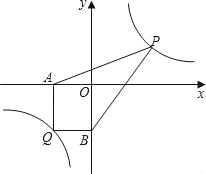
(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数得乘法后,老师给同学们这样一道题目:
计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
聪聪:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
明明:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:29![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
小敏进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为______;
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为______,取得最佳值最小值的数列为______(写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,∠BAD,∠BCD的平分线分别交BC,AD于点F,E.
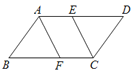
(1)求证:四边形AFCE是平行四边形;
(2)若BF=4,FC=3,求□ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com