
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,.
,.
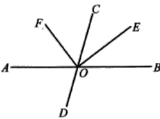
(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求![]() 的度数;
的度数;
(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
【答案】(1)∠AOE和∠DOE;(2)30°;(3)OF平分∠AOC,理由见解析.
【解析】
(1)根据补角的定义可以得出结果,另外注意∠BOE=∠COE,不要漏解;
(2)根据∠COE与∠COF互余,以及∠COF=2∠COE,可以求出∠COE的度数,又OE为∠BOC的平分线可以得出结果;
(3)根据邻补角的性质、角平分线的定义解答.
解:(1)∵OE平分∠BOC,∴∠BOE=∠COE,
∵∠COE+∠DOE=180°,
∴∠BOE+∠DOE=180°.
又∵∠AOE+∠BOE=180°,
所以∠BOE的补角为∠AOE和∠DOE;
(2)∵![]() ,
,
∴∠COE+∠COF=90°,
又∠COF=2∠COE,
∴∠COE=30°.
∴∠BOE=∠COE=30°;
(3)∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°-∠COE.
又∵∠AOF=180°-∠EOF-∠BOE=90°-∠BOE,
又∠BOE=∠COE,
∴∠COF=∠AOF,
∴OF平分∠AOC.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:Rt△ABC中,∠ACB=90°.作∠BAC的平分线AM交BC于点D,在所作图形中,将Rt△ABC沿某条直线折叠,使点A与点D重合,折痕EF交AC于点E,交AB于点F,连接DE、DF,再展回到原图形,得到四边形AEDF.
(1)试判断四边形AEDF的形状,并证明;
(2)若AB=10,BC=8,在折痕EF上有一动点P,求PC+PD的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过原点O及点A(﹣4,0)和点C(2,3).
(1)求抛物线的解析式及顶点坐标;
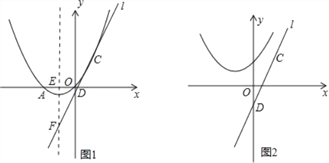
(2)如图1,设抛物线的对称轴与x轴交于点E,将直线y=2x沿y轴向下平移n个单位后得到直线l,若直线l经过C点,与y轴交于点D,且与抛物线的对称轴交于点F.若P是抛物线上一点,且PC=PF,求点P的坐标;
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,求新抛物线上到直线CD距离最短的点的坐标.(直接写出结果,不要解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两。问:每头牛、每只羊各值金多少两?” 设每头牛值金 x 两,每只羊值金 y 两,则列方程组错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的大括号里(将各数用逗号分开):
-8,0.275,![]() ,0,-1.04,-(-3),-
,0,-1.04,-(-3),-![]() ,|-2|.
,|-2|.
(1)正数集合:{ …};
(2)分数集合:{ …};
(3)负整数集合:{ …};
(4)非负数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
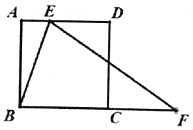
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 上的动点,
上的动点,![]() 是边
是边![]() 延长线上的一点,且
延长线上的一点,且![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)当![]() 是等边三角形时,求
是等边三角形时,求![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
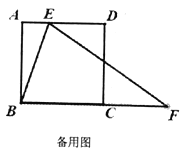
(3)把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,试探索:
处,试探索:![]() 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com