
【题目】已知抛物线y=ax2+bx+c经过原点O及点A(﹣4,0)和点C(2,3).
(1)求抛物线的解析式及顶点坐标;
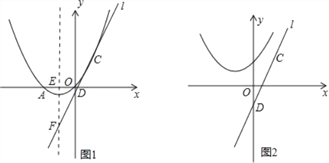
(2)如图1,设抛物线的对称轴与x轴交于点E,将直线y=2x沿y轴向下平移n个单位后得到直线l,若直线l经过C点,与y轴交于点D,且与抛物线的对称轴交于点F.若P是抛物线上一点,且PC=PF,求点P的坐标;
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,求新抛物线上到直线CD距离最短的点的坐标.(直接写出结果,不要解答过程)
【答案】(1) y=![]() x2+x, 顶点坐标为(﹣2,﹣1);(2) (﹣3+
x2+x, 顶点坐标为(﹣2,﹣1);(2) (﹣3+![]() ,
,![]() )或(﹣3﹣
)或(﹣3﹣![]() ,
,![]() );
);
(3) (2,7).
【解析】分析:(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点极坐标;
(2)根据待定系数法,可得直线l的解析式,根据中点坐标公式,可得D是CF的中点,根据勾股定理,可得EF,EC,根据线段垂直平分线的性质,可得ED是线段CF直平分线,根据解方程组,可得P点坐标;
(3)根据平移,可得新抛物线,根据平行于直线与抛物线相切的点到直线的距离最短,可得切线,根据解方程组,可得答案.
详解:(1)∵抛物线y=ax2+bx+c经过原点O及点A(-4,0)和点C(2,3),
∴ ,解得
,解得![]() ,
,
∴抛物线的解析式为y=![]() x2+x;
x2+x;
∵y=![]() x2+x=
x2+x=![]() (x+2)2-1,
(x+2)2-1,
∴抛物线的顶点坐标为(-2,-1);
(2)如图1:

直线l的解析式为y=2x-n,
∵直线l过点C(2,3),
∴n=1,
∴直线l的解析式为y=2x-1,当x=0时,y=-1,即D(0,-1).
∵抛物线的对称轴为x=-2,
∴E(-2,0).
当x=-2时,y=2x-1=-5,即F(-2,-5),
∴CD=DF=2![]() ,
,
∴点D是线段CF的中点,
∵C(2,3),
∴EF=EC=5,
∴ED垂直平分CF.
∴PC=PF,
∴点P在CF的垂直平分线上,
∴点P是抛物线与直线ED的交点.
ED的解析式为y=-![]() x-1.
x-1.
联立抛物线与ED,得
 ,
,
解得 ,
,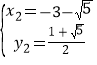 ,
,
点P的坐标(-3+![]() ,
,![]() )或(-3-
)或(-3-![]() ,
,![]() );
);
(3)如图2:

移后的抛物线为y=![]() x2+x+4
x2+x+4
平行于CD与物线相切的直线为y=2x+b,
联立,得![]() x2+x+4=2x+b
x2+x+4=2x+b
方程有相等二实根,得
△=b2-4ac=(-1)2-4×![]() (4-b)=0
(4-b)=0
解得b=3.
![]() x2-x+1=0,
x2-x+1=0,
解得x=2,y=2x+3=7,
新抛物线上到直线CD距离最短的点的坐标是(2,7).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有__________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
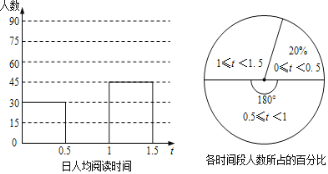
【题目】今年4月23日是第23个“世界读书日”.某校围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是 .
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角是 度.
(4)根据本次抽样调查,试估计我市12000名初二学生中日均阅读时间在0.5~1.5小时的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
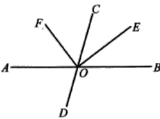
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,.
,.
(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求![]() 的度数;
的度数;
(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=![]()
![]() ,求⊙O半径的长.
,求⊙O半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
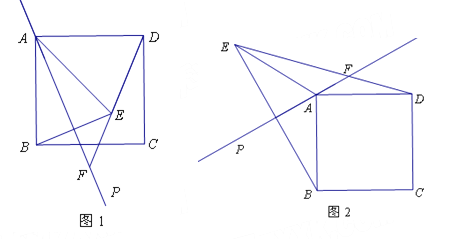
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
(1)(获得结论)在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
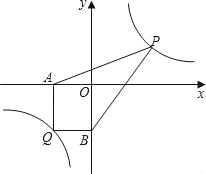
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com