
����Ŀ���ۺ���ʵ��
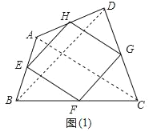
�����龳������ѧ����ϣ����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ���ͼ��1�������ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��˵���е��ı���EFGH��ƽ���ı��Σ�
̽��չʾ���ڷ�С��Ľ���˼·��
��˼������
��1������������˼·�е�������1����������2���ֱ���ʲô��
����1���� ��������2���� ����
������AC����AC��BDʱ�����е��ı���EFGH����״Ϊ�� ����
����С���ܵ��ڷ�С�������������̽����
��2����ͼ��2������P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����˵�����ɣ�
��3�����ı䣨2���е�������ʹ��APB����CPD��90���������������䣬���е��ı���EFGH����״Ϊ�� ����

���𰸡���1��������1�������ε���λ�߶���������2��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ������Σ����ɼ���������2���ı���EFGH�����Σ����ɼ���������3�������Σ����ɼ�����.
��������
��1��������������λ�߶�����ɣ�
��2������ƽ���ı��ε��ж������ε��ж���ɣ�
��3��������һ������ֱ�ǵ������������μ���֤����
��1��������1�������ε���λ�߶�����
����2��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�
������
���ɣ���ͼ1�У�
��AE��BE��AH��HD��
��EH��![]() BD��
BD��
��DH��HA��DG��GC��
��HG��![]() AC��
AC��
��HE��HG��
���ı���EFGH��ƽ���ı��Σ�
���ı���EFGH�����Σ�
�ʴ�Ϊ��������λ�߶�����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ����Σ�
��2�����ۣ��ı���EFGH�����Σ�
���ɣ���ͼ2�У�����AC��BD
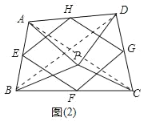
�ߡ�APB����CPD
���APB+��APD����CPD+��APD
������BPD����APC
��PA��PB��PC��PD
���APC�ա�BPD
��AC��BD
��HG��HE
��(1)��֪���ı���EFGH��ƽ���ı���
���ı���EFGH�����Σ�
��3�����ۣ������Σ�
���ɣ���ͼ2��1�У�����AC��BD��BD��AC�ڵ�O����GH�ڵ�K��AC��PD�ڵ�J��
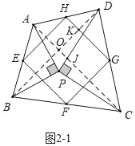
�ߡ�APC�ա�BPD����DPC��90����
���PDB����PCA��
�ߡ�PJC����DJO��
���CPJ����DOJ��90����
��HG��AC��
���BKG����BOC��90����
��EH��BD��
���EHG����BKG��90����
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ����������⣺
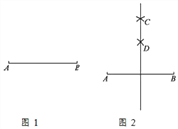
�߹���ͼ����һ���߶εĴ�ֱƽ���ߣ�
��֪���߶�AB��
�������߶�AB�Ĵ�ֱƽ���ߣ�
С����������£�
��ͼ���ٷֱ��Ե�A�͵�BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶�����������ཻ�ڵ�C��
AB�ij�Ϊ�뾶�����������ཻ�ڵ�C��
���ٷֱ��Ե�A�͵�BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶����ͬ�ڢ��еİ뾶�������������ཻ�ڵ�D��ʹ��D���C��ֱ��AB��ͬ�ࣻ
AB�ij�Ϊ�뾶����ͬ�ڢ��еİ뾶�������������ཻ�ڵ�D��ʹ��D���C��ֱ��AB��ͬ�ࣻ
����ֱ��CD��
����ֱ��CD�����������Ĵ�ֱƽ���ߣ�
��ʦ˵����С���������ȷ����
��ش�С�����ͼ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʵ�Ա�ﳵ���ʾֳ��������������� 2 km ���� A �壬������������ 3 km ���� B �壬 Ȼ�������� 9 km ���� C �壬���ص��ʾ�.
(1)���ʾ�Ϊԭ�㣬������Ϊ�������� 1 cm ��ʾ 1 km �����ᣬ���ڸ������ϱ�ʾ A��B��C ������ׯ��λ�ã�
(2)C ���� A ���ж�Զ��
(3)�ʵ�Աһ�������˶���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y=��2x+1�����н�����ȷ���ǣ�������
A. ͼ��ؾ����㣨��2��1�� B. ͼ����һ������������
C. ��x��![]() ʱ��y��0 D. y��x�����������
ʱ��y��0 D. y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���ש��ͼ���������ִ�ש������棬����������ͼ�ڵ�ͼ��������������Բһ����5��������������ͼ�۵�ͼ��������������Բһ����13��������������ͼ�ܵ�ͼ��������������Բһ����25�����Դ˹�����ȥ����10��ͼ�У�������Բһ����__________����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b��ͼ��Ϊֱ��l1������A��0��4����D��4��0�����㣬һ�κ���y��![]() x+1��ͼ��Ϊֱ��l2����x�ύ�ڵ�C����ֱ��l1��l2�ཻ�ڵ�B��
x+1��ͼ��Ϊֱ��l2����x�ύ�ڵ�C����ֱ��l1��l2�ཻ�ڵ�B��
��1����k��b��ֵ��
��2�����B�����ꣻ
��3������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�е������μ����õ�ͼ2����ͼ2�й���4�������Σ���ͼ2�е�һ�������μ����õ�ͼ3��ͼ3�й���7�������Σ���ͼ3��4����С�������е�һ�������õ�ͼ4����ͼ4�й���10�������Σ���������ɼ���ȥ����

��1������ͼ�еĹ��ɲ�ȫ�±���
ͼ�α�� | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
������� | 1 | 4 | 7 | 10 |
|
��2����ڼ���ͼ������2020�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������ת����ת��A��B��ת��A�����ȷֳ�4�ȷݣ�ÿ�ݱ�������1��2��3��4�ĸ����֣�ת��B�����ȷֳ�6�ȷݣ�ÿ�ݱ�������1��2��3��4��5��6�������֣�����Ϊ�������������һ����Ϸ����������£�
ͬʱת��ת��A��B��ת��ֹͣ��ָ���ָ��һ�����֣����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��һ������Ϊֹ��������ָ�������������˻���������õĻ���ż������ô��1�֣�������õĻ�����������ô�ҵ�1�֣�����Ϊ�����Ĺ����Ƿ�ƽ������˵�����ɣ��������ƽ�������Ĺ���ʹ����Ϸ��˫����ƽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
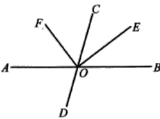
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��.
��.
(1)ͼ�С�BOE�IJ�����
(2)����COF��2��COE����![]() �Ķ���;
�Ķ���;
(3) ���ж�OF�Ƿ�ƽ�֡�AOC����˵�����ɣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com