练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】关于函数y=﹣2x+1，下列结论正确的是（　　）

    A. 图象必经过点（﹣2，1） B. 图象经过第一、二、三象限

    C. 当x＞时，y＜0 D. y随x的增大而增大

    【答案】C

    【解析】根据一次函数的性质，依次分析可得，

    A.x=2时,y=2×2+1=5,故图象必经过(2,5)，故错误，

    B.k<0，则y随x的增大而减小，故错误，

    C. 当x>时，y<0，正确；

    D.k=2<0，b=1>0，则图象经过第一、二、四象限，故错误，

    故选C.

    点睛:本题考查了一次函数的图象以及一次函数的性质,解题的关键是逐条分析四个选项.本题属于基础题,难度不大,解决该题时,熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD中，AB=1，∠A=60°，EFGH是矩形，矩形的顶点都在菱形的边上．设AE=AH=x（0＜x＜1），矩形的面积为S．

    （1）求S关于x的函数解析式；

    （2）当EFGH是正方形时，求S的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1x1,y1，P2x2,y2，可通过构造直角三角形利用图1得到结论：，他还利用图2证明了线段P1P2的中点Px,y的坐标公式：

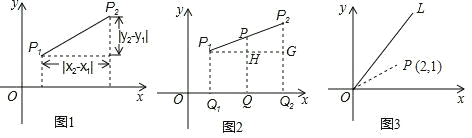
    （1）已知点M2,1,N2,5，则线段MN长度为 ；

    （2）请求出以点A2,2,B2,0,C3,1，D为顶点的平行四边形顶点D的坐标；

    （3）如图3，OL满足y2xx0，点P2,1是OL与x轴正半轴所夹的内部一点，请在OL、x轴上分别找出点E、F，使PEF的周长最小，求出周长的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

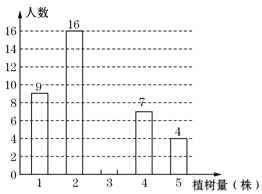
    【题目】为了发展乡村旅游，建设美丽从化，某中学七年级一班同学都积极参加了植树活动，今年四月份该班同学的植树情况部分如图所示，且植树2株的人数占32%．

    （1）求该班的总人数、植树株数的众数，并把条形统计图补充完整；

    （2）若将该班同学的植树人数所占比例绘制成扇形统计图时，求“植树3株”对应扇形的圆心角的度数；

    （3）求从该班参加植树的学生中任意抽取一名，其植树株数超过该班植树株数的平均数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是直角三角形，∠ACB=90°．

    （1）尺规作图：作⊙C，使它与AB相切于点D，与AC相交于点E，保留作图痕迹，不写作法，请标明字母．

    （2）在你按（1）中要求所作的图中，若BC=3，∠A=30°，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

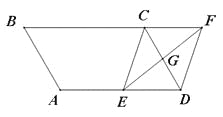
    【题目】（7分）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

    （1）求证：四边形CEDF是平行四边形；

    （2）①当AE= cm时，四边形CEDF是矩形；

    ②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    问题情境：在数学活动课上，我们给出如下定义：顺次连按任意一个四边形各边中点所得的四边形叫中点四边形．如图（1），在四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．试说明中点四边形EFGH是平行四边形．

    探究展示：勤奋小组的解题思路：

    反思交流：

    （1）①上述解题思路中的“依据1”、“依据2”分别是什么？

    依据1：　 　；依据2：　 　；

    ②连接AC，若AC＝BD时，则中点四边形EFGH的形状为　 　；

    创新小组受到勤奋小组的启发，继续探究：

    （2）如图（2），点P是四边形ABCD内一点，且满足PA＝PB，PC＝PD，∠APB＝∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并说明理由；

    （3）若改变（2）中的条件，使∠APB＝∠CPD＝90°，其它条件不变，则中点四边形EFGH的形状为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．

    （1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；

    （2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；

    （3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值．例：点A、B在数轴上对应的数分别为a、b，则A、B两点间的距离表示为AB＝|a﹣b|．根据以上知识解题：

    （1）点A在数轴上表示3，点B在数轴上表示2，那么AB＝_______．

    （2）在数轴上表示数a的点与﹣2的距离是3，那么a＝______．

    （3）如果数轴上表示数a的点位于﹣4和2之间，那么|a+4|+|a﹣2|＝______．

    （4）对于任何有理数x，|x﹣3|+|x﹣6|是否有最小值？如果有，直接写出最小值．如果没有．请说明理由．

    查看答案和解析>>

    同步练习册答案