
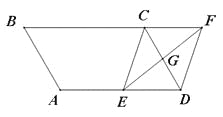
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
【答案】(1)证明见解析;
(2)① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.
【解析】
试题(1)利用“ASA”即可得证;
①当四边形CEDF是矩形时,则有EG=DG=1.5cm,又由已知可得∠ADC=60°,从而得△EGD为等边三角形,从而得DE=1.5cm,从而得AE=3.5cm;
②.当四边形CEDF是菱形时,则有EF⊥CD,由已知可知∠ADC=60°,从而可得∠DEG=30°,从而得DE=2DG=3,从而得AE=2.
试题解析:(1)∵ 四边形ABCD是平行四边形, ∴ CF∥ED, ∴ ∠FCG=∠EDG,∵ G是CD的中点,∴ CG=DG,在△FCG和△EDG中,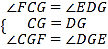 ,∴ △FCG ≌△EDG(ASA),∴ FG=EG,∵ CG=DG,∴ 四边形CEDF是平行四边形;
,∴ △FCG ≌△EDG(ASA),∴ FG=EG,∵ CG=DG,∴ 四边形CEDF是平行四边形;
(2)① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.


科目:初中数学 来源: 题型:
【题目】计算题
(1)(3ab)2(﹣![]() ab3)
ab3)
(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( ) .
A.AC⊥BDB.四边形ABCD是菱形
C.AC=BCD.△ABO≌△CDO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 ( ) .

A.4.8B.3![]() C.5D.3
C.5D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放以来,我国国民经济保持良好发展势头,国内生产总值持续较快增长, 下图是1998年~2002年国内生产总值统计图.

(1)从图中可看出1999年国内生产总值是___________.
(2)已知2002年国内生产总值比2000年增加12956亿元,2001年比2000年增加6491亿元,求2002年国内生产总值比2001年增长的百分率(结果保留两个有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买12台节能新设备,现有甲乙两种型号的设备可供选购,经调查,购4台甲比购3台乙多用18万元,购3台甲比购4台乙少用4万元。
(1)求甲乙两种设备的单价。
(2)该公司决定购买甲设备不少于5台,购买资金不超过136万元,你认为该公司有几种购买方案?并直接写出最省钱的购买方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com