
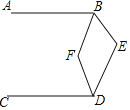
【题目】如图,![]() 平分
平分![]() 平分
平分![]() ,则
,则![]() ______ .
______ .
【答案】![]()
【解析】
首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两只线平行,内错角相等,即可求得∠BFD的度数.
过点E作EM∥AB,过点F作FN∥AB,
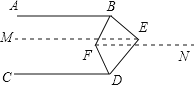
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=125°,
(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故答案为125°


科目:初中数学 来源: 题型:
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
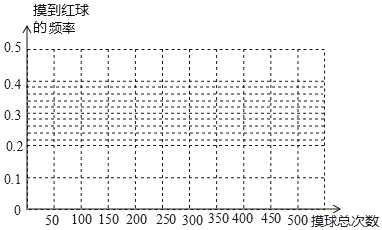
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感恩节即将来临,小王调查了初三年级部分同学在感恩节当天将以何种方式对帮助过自己的人表达感谢,他将调查结果分为如下四类:A类﹣﹣当面表示感谢、B类﹣﹣打电话表示感谢、C类﹣﹣发短信表示感谢、D类﹣﹣写书信表示感谢.他将调查结果绘制成了如图所示的扇形统计图和条形统计图.请你根据图中提供的信息完成下列各题:
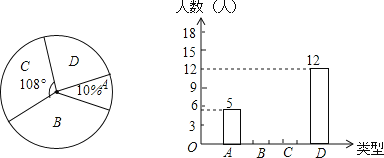
(1)补全条形统计图;
(2)在A类的同学中,有4人来自同一班级,其中有2人主持过班会.现准备从他们4人中随机抽出两位同学主持感恩节主题班会课,请用树状图或列表法求抽出1人主持过班会而另一人没主持过班会的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) ![]()
(2)(2a3b-4ab3)·(-![]() ab)-(-2a2)2(-b2)
ab)-(-2a2)2(-b2)
(3)先化简,再求代数式(a+2b)(a-2b)+(a+2b)2-4ab 的值,其中 a=1,b=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
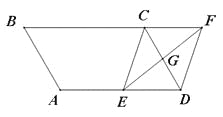
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为第三象限内一点.
为第三象限内一点.

(1)若![]() 到坐标轴的距离相等,
到坐标轴的距离相等,![]() ,且
,且![]() ,求
,求![]() 点坐标
点坐标
(2)若![]() 为
为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() 的面积.
的面积.
(3)在(2)条件下,当![]() 时,在
时,在![]() 轴上有点
轴上有点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍,请求出点
的面积的2倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
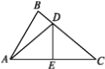
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com