
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
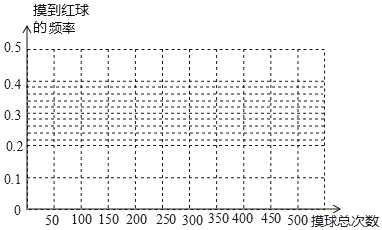
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】新定义:在平面直角坐标系![]() 中,对于任意点
中,对于任意点![]() ,和直线
,和直线![]() ,我们称直线
,我们称直线![]() 为点
为点![]() 的伴随直线,反之称点
的伴随直线,反之称点![]() 为直线
为直线![]() 的伴随点;特别的,直线
的伴随点;特别的,直线![]() (
(![]() 为常数)的伴随点为
为常数)的伴随点为![]() .
.


如图1,已知![]() 三个顶点
三个顶点![]() 的坐标分别为
的坐标分别为![]() .
.
(1)点![]() 的伴随直线的解析式为__________.(请直接写出答案)
的伴随直线的解析式为__________.(请直接写出答案)
(2)若直线![]() 的伴随点是点
的伴随点是点![]() ,直线
,直线![]() 的伴随点是点
的伴随点是点![]() ,点
,点![]() 为
为![]() 轴上的动点,当
轴上的动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标.
的坐标.
(3)点![]() 是折线段
是折线段![]() 的动点(包括端点
的动点(包括端点![]() ),若直线
),若直线![]() 是点
是点![]() 的伴随直线,当直线
的伴随直线,当直线![]() 与
与![]() 有且仅有两个公共点时,请直接写出点
有且仅有两个公共点时,请直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(3ab)2(﹣![]() ab3)
ab3)
(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为线段
为线段![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),分别以
重合),分别以![]() 为一腰在
为一腰在![]() 的同侧作等腰
的同侧作等腰![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
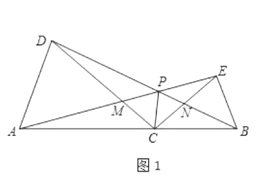
![]() 线段
线段![]() 与
与![]() 的数量关系为 ;请直接写出
的数量关系为 ;请直接写出![]() ;
;
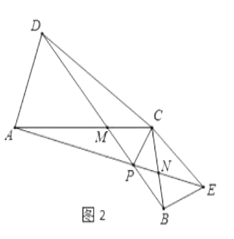
![]() 将
将![]() 绕点
绕点![]() 旋转到如图2所示的位置,其他条件不变,探究线段
旋转到如图2所示的位置,其他条件不变,探究线段![]() 与
与![]() 的数量关系,并说明理由;求出此时
的数量关系,并说明理由;求出此时![]() 的度数;
的度数;
![]() 在
在![]() 的条件下求证:
的条件下求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
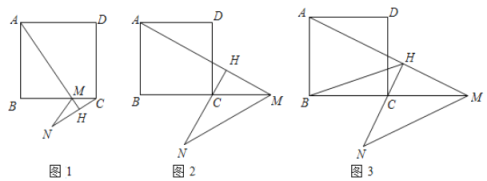
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com