
【题目】如图1,点![]() 为线段
为线段![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),分别以
重合),分别以![]() 为一腰在
为一腰在![]() 的同侧作等腰
的同侧作等腰![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
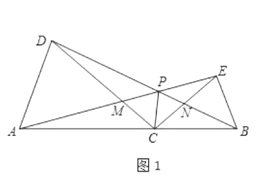
![]() 线段
线段![]() 与
与![]() 的数量关系为 ;请直接写出
的数量关系为 ;请直接写出![]() ;
;
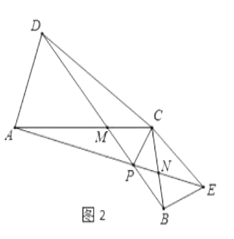
![]() 将
将![]() 绕点
绕点![]() 旋转到如图2所示的位置,其他条件不变,探究线段
旋转到如图2所示的位置,其他条件不变,探究线段![]() 与
与![]() 的数量关系,并说明理由;求出此时
的数量关系,并说明理由;求出此时![]() 的度数;
的度数;
![]() 在
在![]() 的条件下求证:
的条件下求证:![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() ,
,![]() ,理由见解析;(3)见解析
,理由见解析;(3)见解析
【解析】
(1)只要证明△ACE≌△DCB,即可解决问题;
(2)只要证明△ACE≌△DCB,即可解决问题;
(3)如图2-1中,分别过C作CH⊥AE,垂足为H,过点C作CG⊥BD,垂足为G,利用面积法证明CG=CH,再利用角平分线的判定定理证明∠DPC=∠EPC即可解决问题;
![]() 如图1中,
如图1中,

∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMC=∠DMP,
∴∠APD=∠ACD=30°,
故答案为AE=BD,30°
![]() 如图2中,结论:
如图2中,结论:![]() ,
,![]() .
.
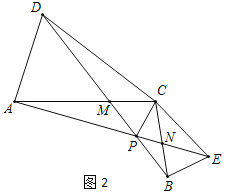
理由:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMP=∠DMC,
∴∠APD=∠ACD=30°.
![]() 证明:如图2-1中,分别过
证明:如图2-1中,分别过![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
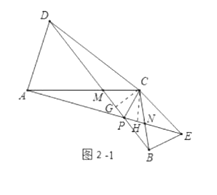
∵△ACE≌△DCB.
∴AE=BD,
∵S△ACE=S△DCB(全等三角形的面积相等),
∴CH=CG,
∴∠DPC=∠EPC(角平分线的性质定理的逆定理),
∵∠APD=∠BPE,
∴∠APC=∠BPC.


科目:初中数学 来源: 题型:
【题目】学校某社团为了调查同学们上学时所使用交通工具的情况,随机抽取了部分同学进行调查,要求调查者从“![]() :公交车”“
:公交车”“![]() :家庭汽车”“
:家庭汽车”“![]() :地铁”“
:地铁”“![]() :自行车”“
:自行车”“![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如图所示的不完整条形统计图和扇形统计图,请结合统计图解答下列问题:
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如图所示的不完整条形统计图和扇形统计图,请结合统计图解答下列问题:

(1)表示![]() 组的扇形统计图所对应的圆心角是________度,补全条形统计图;
组的扇形统计图所对应的圆心角是________度,补全条形统计图;
(2)若社团想从![]() 组的甲、乙,丙、丁四人中随机选择两人,了解他们使用的电动车品牌情况,请用列表或画树状图的方法求出恰好选中乙的概率.
组的甲、乙,丙、丁四人中随机选择两人,了解他们使用的电动车品牌情况,请用列表或画树状图的方法求出恰好选中乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
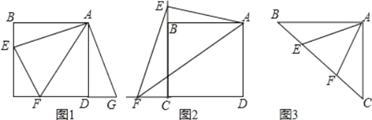
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是____________.


(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使![]() ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
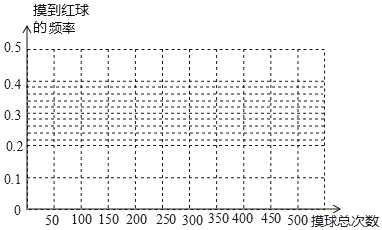
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
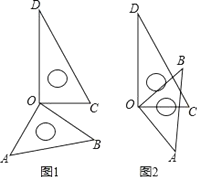
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板![]() 和
和![]() 拼合在一起,边
拼合在一起,边![]() 与
与![]() 重合,
重合,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 向下滑动时,点
向下滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 向右滑动.当点
向右滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,连接
时,连接![]() ,则
,则![]() 的面积最大值为_______
的面积最大值为_______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为第三象限内一点.
为第三象限内一点.

(1)若![]() 到坐标轴的距离相等,
到坐标轴的距离相等,![]() ,且
,且![]() ,求
,求![]() 点坐标
点坐标
(2)若![]() 为
为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() 的面积.
的面积.
(3)在(2)条件下,当![]() 时,在
时,在![]() 轴上有点
轴上有点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的2倍,请求出点
的面积的2倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com