
【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
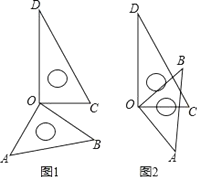
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
【答案】(1)①∠AOC与∠BOD相等,见解析;②∠AOD+∠BOC=180°,见解析;(2)①∠AOB=∠COD,∠AOC=∠BOD;②∠AOB与∠COD,∠AOD与∠BOC,见解析.
【解析】
(1)①根据等式的性质解答即可;②根据周角的定义解答即可;(2)根据余角和补角的概念、结合图形解答即可.
(1)①∠AOC与∠BOD相等.
理由如下:∵∠AOB=∠DOC=90°,
∴∠AOB+∠BOC=∠DOC+∠BOC,
即∠AOC=∠BOD;
②∵∠AOD+∠BOC+∠COD+∠AOB=360°,
∴∠AOD+∠BOC=180°;
(2)①∠AOB=∠COD,∠AOC=∠BOD;
②∠AOB+∠COD=180°,∠AOD+∠BOC=180°.
理由如下:
∵∠AOB=90°,∠DOC=90°,
∴∠AOB+∠DOC=180
∵∠DOC=∠BOC+∠BOD
∴∠AOB+∠BOC+∠BOD=180°
∴∠AOD+∠BOC=180°


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为线段
为线段![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),分别以
重合),分别以![]() 为一腰在
为一腰在![]() 的同侧作等腰
的同侧作等腰![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
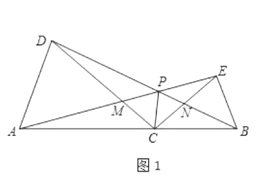
![]() 线段
线段![]() 与
与![]() 的数量关系为 ;请直接写出
的数量关系为 ;请直接写出![]() ;
;
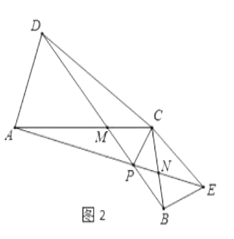
![]() 将
将![]() 绕点
绕点![]() 旋转到如图2所示的位置,其他条件不变,探究线段
旋转到如图2所示的位置,其他条件不变,探究线段![]() 与
与![]() 的数量关系,并说明理由;求出此时
的数量关系,并说明理由;求出此时![]() 的度数;
的度数;
![]() 在
在![]() 的条件下求证:
的条件下求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
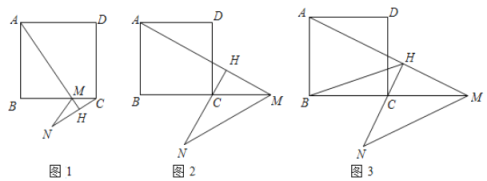
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,可推得
,可推得![]() .理由如下:
.理由如下:
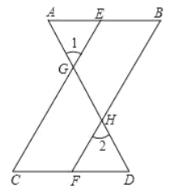
![]()
![]() (已知),
(已知),
且![]() (________)
(________)
![]()
![]() (等量代换)
(等量代换)
![]()
![]() (________)
(________)
![]()
![]() ________
________![]() (________)
(________)
又![]()
![]() (已知)
(已知)
![]()
![]() (等量代换)
(等量代换)
![]()
![]() (________)
(________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com