
【题目】如图,矩形纸片![]() ,对角线为
,对角线为![]() ,沿过点
,沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() ,若
,若![]() ,则
,则![]() 的长是( )
的长是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由折叠即可得∠GDA=∠GDB,AD=ED,然后过点G作GE⊥BD于E,即可得AG=EG,设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,在Rt△BEG中利用勾股定理,即可求得AG的长.
根据题意可得:∠GDA=∠GDB,AD=ED,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3,
∴AG=EG,ED=3,
∵AB=4,BC=3,∠A=90°,
∴BD=5,
设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,
在Rt△BEG中,EG2+BE2=BG2,
即:x2+4=(4-x)2,
解得:x=![]() ,
,
∴AG=![]() .
.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学习了统计知识后,小刚就本班同学的三种上学方式进行了一次全面调查,每位同 学选择其中一种方式,图①和图②是他通过收集数据后,绘制的两幅不完整的统计 图:
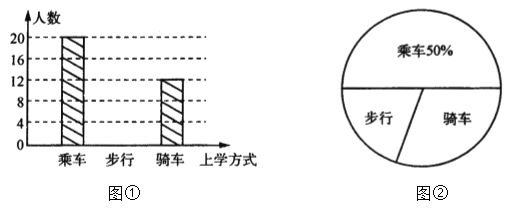
请你根据以上信息解答下列问题:
(1)该班共有多少名学生?
(2)在扇形图中,骑车上学的人数占全班总人数的百分比是多少?
(3)在条形图中,将表示“步行”上学方式的部分补充完整;
(4)如果全年级共 500 名学生,请你估计全年级步行上学的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求菱形的周长.
(3)在(2)的基础上,直接写出BD与EF的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
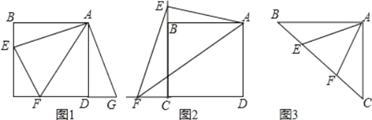
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是____________.


(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使![]() ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
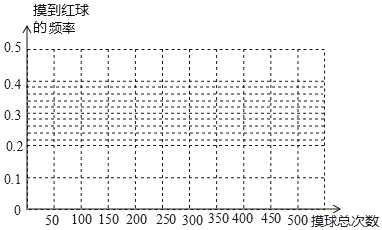
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
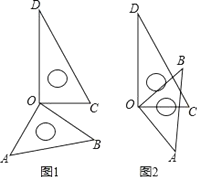
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) ![]()
(2)(2a3b-4ab3)·(-![]() ab)-(-2a2)2(-b2)
ab)-(-2a2)2(-b2)
(3)先化简,再求代数式(a+2b)(a-2b)+(a+2b)2-4ab 的值,其中 a=1,b=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com