Question

【题目】学习了统计知识后，小刚就本班同学的三种上学方式进行了一次全面调查，每位同 学选择其中一种方式，图①和图②是他通过收集数据后，绘制的两幅不完整的统计 图：

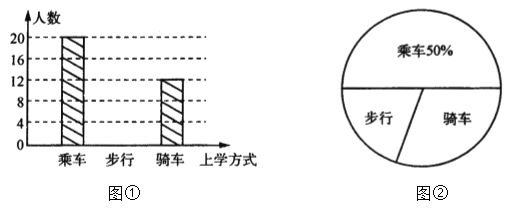
请你根据以上信息解答下列问题：

（1）该班共有多少名学生？

（2）在扇形图中，骑车上学的人数占全班总人数的百分比是多少？

（3）在条形图中，将表示“步行”上学方式的部分补充完整；

（4）如果全年级共 500 名学生，请你估计全年级步行上学的学生有多少人.

Answer 1

【答案】（1）40人；（2）；（3）见解析；（4）100名

【解析】

（1）乘车的有20人，所占百分比为50%，即可求出该班总人数；

（2）用骑车人数除以样本容量即可；

（3）用样本容量减去乘车人数和骑车人数求出步行人数，补全统计图即可；

（3）总人数×步行上学所占百分比即可求得结果．

解：（1）∵乘车的人数是20人，所占的百分比是50%，

∴该班共有学生数是：20÷50%=40人；

（2）骑车的人数为15人，所占的比分比是；

（3）40-20-12=8人，

如图，

（4）步行所占的比分比是100％-50％-30％=20％

“步行”学生人数：500×20%=100名，