
����Ŀ����֪�ٺϾƵ�����˼��˫�˼�ͷ����Ϊ�����˼�Ϊÿ��ÿ��200Ԫ��˫�˼�Ϊÿ��ÿ��300Ԫ��Ϊ������Դ���ٽ����Σ��ڡ�ʮһ���ƽ����ڼ�Ƶ�����Żݴ�������������סһ�������Ż�.һ��50�˵���������ʮ�¶��ŵ��þƵ�ס�ޣ���ס��һЩ���˼䡢˫�˼�ͷ���
��1�������ס��ÿ���ͷ�����ס��������һ��һ����ȥס��6300Ԫ.����ס�����˼䡢˫�˼�ͷ������ټ䣿
��2�������˼乲ס��x�ˣ������һ��һ����ȥס��yԪ����д��y��x�ĺ�����ϵʽ��
��3��һ��6300Ԫ��ס���Ƿ�Ϊ��ͣ�������ǣ������һ�ַ�����Ҫ����ס�ķ������ñ�ס���ģ���ʹס������ͣ���д����Ʒ������������͵ķ��ã�
���𰸡���1��8�䣬13�� ��2��![]() ����3�����ǣ����˿ͷ�16�䣬˫�˿ͷ�1��ʱ������ͣ���ͷ���Ϊ5100Ԫ��
����3�����ǣ����˿ͷ�16�䣬˫�˿ͷ�1��ʱ������ͣ���ͷ���Ϊ5100Ԫ��
��������
(1)�����˼���![]() �䣬˫�˼���
�䣬˫�˼���![]() �䣮ע�ⷲ������סһ�������Żݣ����ݢٿͷ�����=50����ס��6300 �з�������⣻
�䣮ע�ⷲ������סһ�������Żݣ����ݢٿͷ�����=50����ס��6300 �з�������⣻
(2)�������⣬���˼�ס��![]() �ˣ���˫�˼�ס��(
�ˣ���˫�˼�ס��(![]() )�ˣ�ס��=100�����˼������+150��˫�˼��������
)�ˣ�ס��=100�����˼������+150��˫�˼��������
(3)����![]() ��ȡֵ��Χ��ʵ����������ú��������ʽ��
��ȡֵ��Χ��ʵ����������ú��������ʽ��
(1)�����˼���![]() �䣬˫�˼���
�䣬˫�˼���![]() �䣬
�䣬
��������ã�![]() ��
��
��ã�![]() ��
��
����ס�����˼�8�䣬˫�˼�13�䣻
(2)�������⣬���˼�ס��![]() �ˣ�ס��ÿ��100Ԫ����˫�˼�ס��(
�ˣ�ס��ÿ��100Ԫ����˫�˼�ס��(![]() )�ˣ�ס��ÿ��150Ԫ��
)�ˣ�ס��ÿ��150Ԫ��
��![]() ��
��
(3)��Ϊ![]() ������
������![]() ��
��![]() �����������
�����������
�ʵ�![]() ����
����![]() ��
��![]() ��������
Ϊ��������![]() ���ʱ��
���ʱ��
��![]() ʱ��ס������ͣ�
ʱ��ס������ͣ�
��ʱ![]() ��
��
��һ��6300Ԫ��ס�Ѳ�����ͣ���48����ס���˼䣬�������ͣ�Ϊ5100Ԫ��
����ס������͵���Ʒ���Ϊ��48��ס3�˼䣬2��ס2�˼䣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��2��1����B����1��1����C����1����3����D��2����3������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���A��B��C��D��A���Ĺ�����ͼ����ABCD�ı���ѭ���˶������2019��ʱ��P������Ϊ��������

A. ��1��1��B. ��0��1��C. ����1��1��D. ��2����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ֱ��������ABC��AB����ƽ�Ƶõ�ֱ��������DEF,��֪BE=3,BE=3,FG=1,AC=5,��ͼ����Ӱ���ֵ����Ϊ�� ��
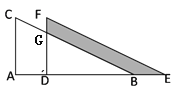
A.10B.13.5C.20D.9.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��27�ľ��루B��F��C��һ��ֱ���ϣ���

��1����칫¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ��룮
���ο����ݣ�sin22����![]() ��cos22����
��cos22����![]() ��tan22����
��tan22����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AC=BC=1����C=90����E��F��AB�ϵĶ��㣬����ECF=45�����ֱ��E��F��BC��AC�Ĵ��ߣ�����ֱ�ΪH��G�������߽��ڵ�M��

��1������E���B�غ�ʱ����ֱ��д��MH��AC��������ϵ ��
��2��̽��AF��EF��BE֮���������ϵ����֤����Ľ��ۣ�
��3����CΪ����ԭ�㣬��BC���ڵ�ֱ��Ϊx�ᣬ����ֱ������ϵ���뻭������ϵ�����ã�2���еĽ���֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+1�����㣨2��6��������ֱ��y=![]() x+1�ཻ��A��B���㣬��A��y���ϣ�����B��BC��x�ᣬ����Ϊ��C��4��0����
x+1�ཻ��A��B���㣬��A��y���ϣ�����B��BC��x�ᣬ����Ϊ��C��4��0����

��1���������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ����������ϵ�һ�����㣬����P��PD��x���ڵ�D����AB�ڵ�E�����߶�PE�����ֵ��
��3���ڣ�2������������PC��AB�ཻ�ڵ�Q�����߶�PC��BE�ƽ��ʱ���������Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ��ͳ��֪ʶ��С�վͱ���ͬѧ��������ѧ��ʽ������һ��ȫ����飬ÿλͬ ѧѡ������һ�ַ�ʽ��ͼ�ٺ�ͼ������ͨ���ռ����ݺ��Ƶ�������������ͳ�� ͼ��
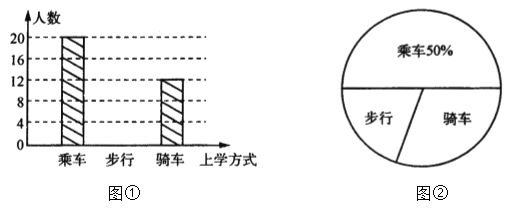
�������������Ϣ����������⣺
��1���ð�ж�����ѧ����
��2��������ͼ�У��ﳵ��ѧ������ռȫ���������İٷֱ��Ƕ��٣�
��3��������ͼ�У�����ʾ����������ѧ��ʽ�IJ��ֲ���������
��4�����ȫ�꼶�� 500 ��ѧ�����������ȫ�꼶������ѧ��ѧ���ж�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��6��BC��4�����Խ���BD�е�O��ֱ�߷ֱ�AB��CD���ڵ�E��F.
��1����֤���ı���DEBF��ƽ���ı��Σ�
��2�����ı���DEBF������ʱ�������ε��ܳ���
��3���ڣ�2���Ļ����ϣ�ֱ��д��BD��EF��λ�ù�ϵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com