[题目]式子的计算结果的个位数上的数字( )A.1B.3C.7D.9 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】式子的计算结果的个位数上的数字（）

A.1B.3C.7D.9

【答案】A

【解析】

原式中2变形为（3-1）后，利用平方差公式计算即可得到结果．

原式=(31)(3+1)(3 +1)(3 +1)(3 +1)(3 +1)(3 +1)+1

=(31)(3+1)(3+1)(3+1)(3+1)(3+1)+1

=(31)(3+1)(3+1)(3+1)(3+1)+1

=(31)(3+1)(3+1)(3+1)+1

=(31)(3+1)(3+1)+1

=(31)(3+1)+1

=3 1+1

=3.

3 的个位数字为3，3 的个位数字为9，3 的个位数字为7，3 的个位数字为1，3 的个位数字为3，…

即3的个位数字，以3、9、7、1为一组循环出现.

∵64÷4=16，

∴3的个位数字为1，即原式个位数字为1.

故选A.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，在直角三角形ABC中，∠ABC=90，将三角形ABC绕着点B逆时针旋转一定角度得到三角形BEF，EF交BC于点G．

（1）若，当∠ABE等于多少度时，；

（2）若，，，当时，

①求BG的长；

②连接AF交BE于点O，连接AE（如图2），设三角形EOF的面积为m，求三角形AEO的面积（用含m的代数式表示）

查看答案和解析>>

科目：初中数学 来源： 题型：

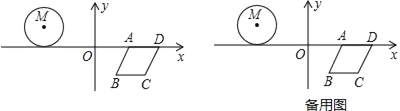
【题目】如图，⊙M与菱形ABCD在平面直角坐标系中，点M的坐标为（﹣3，1），点A的坐标为（2，0），点B的坐标为（1，﹣），点D在x轴上，且点D在点A的右侧．

（1）求菱形ABCD的周长；

（2）若⊙M沿x轴向右以每秒2个单位长度的速度平移，菱形ABCD沿x轴向左以每秒3个单位长度的速度平移，设菱形移动的时间为t（秒），当⊙M与AD相切，且切点为AD的中点时，连接AC，求t的值及∠MAC的度数；

（3）在（2）的条件下，当点M与AC所在的直线的距离为1时，求t的值．

【答案】（1）菱形的周长为8；（2）t=，∠MAC=105°；（3）当t=1﹣或t=1+时，圆M与AC相切．

【解析】试题分析：（1）过点B作BE⊥AD，垂足为E．由点A和点B的坐标可知：BE=，AE=1，依据勾股定理可求得AB的长，从而可求得菱形的周长；（2）记 M与x轴的切线为F，AD的中点为E．先求得EF的长，然后根据路程=时间×速度列出方程即可；平移的图形如图3所示：过点B作BE⊥AD，垂足为E，连接MF，F为 M与AD的切点．由特殊锐角三角函数值可求得∠EAB=60°，依据菱形的性质可得到∠FAC=60°，然后证明△AFM是等腰直角三角形，从而可得到∠MAF的度数，故此可求得∠MAC的度数；（3）如图4所示：连接AM，过点作MN⊥AC，垂足为N，作ME⊥AD，垂足为E．先求得∠MAE=30°，依据特殊锐角三角函数值可得到AE的长，然后依据3t+2t=5-AE可求得t的值；如图5所示：连接AM，过点作MN⊥AC，垂足为N，作ME⊥AD，垂足为E．依据菱形的性质和切线长定理可求得∠MAE=60°，然后依据特殊锐角三角函数值可得到EA=，最后依据3t+2t=5+AE．列方程求解即可．

试题解析：（）如图1所示：过点作，垂足为，

∵，，

∴，，

∴，

∵四边形为菱形，

∴，

∴菱形的周长．

（）如图2所示，⊙与轴的切线为，中点为，

∵，

∴，

∵，且为中点，

∴，，

∴，

解得．

平移的图形如图3所示：过点作，

垂足为，连接，为⊙与切点，

∵由（）可知，，，

∴，

∵四边形是菱形，

∴，

∵为切线，

∴，

∵为的中点，

∴，

∴是等腰直角三角形，

∴，

∴．

（）如图4所示：连接，过点作，垂足为，作，垂足为，

∵四边形为菱形，，

∴．

∵、是圆的切线

∴，

∵。

∴，

∴．

如图5所示：连接，过点作，垂足为，作，垂足为，

∵四边形为菱形，，

∴，

∵、是圆的切线，

∴，

∵，

∴，

∴．

综上所述，当或时，圆与相切．

点睛：此题是一道圆的综合题.圆中的方法规律总结：1、分类讨论思想：研究点、直线和圆的位置关系时，就要从不同的位置关系去考虑，即要全面揭示点、直线和元的各种可能的位置关系.这种位置关系的考虑与分析要用到分类讨论思想.1、转化思想：（1）化“曲面”为“平面”（2）化不规则图形面积为规则图形的面积求解.3、方程思想：再与圆有关的计算题中，除了直接运用公式进行计算外，有时根据图形的特点，列方程解答，思路清楚，过程简捷.

【题型】解答题
【结束】
28

【题目】如图1，在平面直角坐标系中，直线l与x轴、y轴分别交于点B（4，0）、C（0，3），点A为x轴负半轴上一点，AM⊥BC于点M交y轴于点N（0，）．已知抛物线y=ax2+bx+c经过点A，B，C．