
����Ŀ��Ϊ�˽�ij��������һ�ܿ����Ķ�ʱ��������������ȡ������ѧ�����е��飬���ݵ����������Ķ�ʱ����Ϊ���ࣺ2Сʱ���ڣ�2��4Сʱ����2Сʱ����4��6Сʱ����4Сʱ����6Сʱ�����ϣ�����������ͼ��ʾ��������ͳ��ͼ��

��1�����ε��鹲�����ȡ�� ��ѧ����
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�У������Ķ�ʱ����4��6Сʱ����Ӧ��Բ�ĽǶ���Ϊ ![]() ��
��
��4������������10 000�������������Ƹõ�����ѧ��һ�ܿ����Ķ�ʱ��������4Сʱ��������
���𰸡���1��200����2��ͼ����������3��144����4��6 500��
��������
��1�����Ķ�ʱ���ڡ�6Сʱ�����ϡ����������Զ�Ӧ�ٷֱȼ��ɼ��㣻
��2���ȸ���ͳ��ͼ�е�������������Ķ�ʱ���ڡ�2~4Сʱ���͡�4~6Сʱ����������Ȼ��ȫ����ͳ��ͼ���ɣ�
��3����360����Կ����Ķ�ʱ����4��6Сʱ����Ӧ�İٷֱȼ��������
��4���ó�������������һ�ܿ����Ķ�ʱ��������4Сʱ�İٷֱȼ��ɣ�
��1�����ε��鹲�����ȡ�ˣ�50��25%=200��������
��2�������Ķ�ʱ����2~4Сʱ�����У�200��20%=40���ˣ���
�����Ķ�ʱ����4~6Сʱ�����У�200-30-40-50=80���ˣ���
������ͳ��ͼ���£�
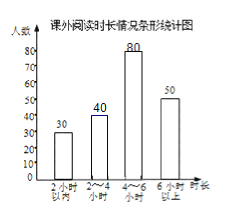 ��
��
��3���Ķ�ʱ���ڡ�2Сʱ���ڡ���������ռ�İٷֱ�Ϊ��30��200��100%=15%��
�����Ķ�ʱ����4~6Сʱ����Ӧ��Բ�ĽǶ���Ϊ��360�����1-20%-25%-15%��=144�㣻
��4��10000����1-20%-15%��=6500���ˣ���


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
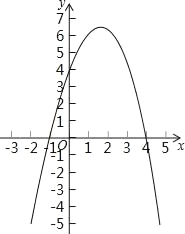
����Ŀ����֪���κ���y=��x2+3x+4��ͼ����ͼ����ֱ��д�𰸣�
��1�����̩�x2+3x+4=0�Ľ����� ����
��2������ʽ��x2+3x+4��0�Ľ⼯���� ����
��3������ʽ��x2+3x+4��0�Ľ⼯���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �еĵ�
�еĵ�![]() ������
������![]() ������Ϊ
������Ϊ![]() ������
������![]() ��������
Ϊ��������![]() ������Ƶ�
������Ƶ�![]() Ϊ��
��![]() ����
����![]() ����������.���磺
����������.���磺![]() ����2����������Ϊ
����2����������Ϊ![]() ����
����![]() .
.
��l�����![]() ����3����������
����3����������![]() �����꣺
�����꣺
��2������![]() ����5����������
����5����������![]() ������Ϊ
������Ϊ![]() �����
�����![]() �����꣺
�����꣺
��3������![]() ��
��![]() ����������ϣ���
����������ϣ���![]() ����������������Ϊ
����������������Ϊ![]() �㣬���߶�
�㣬���߶�![]()
![]() �ij���Ϊ�߶�
�ij���Ϊ�߶�![]() ���ȵ�2������k��ֵ.
���ȵ�2������k��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ͳ�������ͬ�����µķ�ѿʵ�������±���
ÿ������n | 100 | 150 | 200 | 500 | 800 | 1 000 |
��ѿ������m | 65 | 111 | 136 | 345 | 560 | 700 |
��ѿ��Ƶ�� | 0.65 | 0.74 | 0.68 | 0.69 | a | b |
��1��a�� ��b�� ��
��2�������Ͳ��ѷ�ѿ�ĸ��ʹ���ֵ�Ƕ��٣����Ҫ˵�����ɣ�
��3����������Ͳ��ѷ�ѿ��ij�����Ϊ90%��������ͬ��������10 000�������Ͳ��ѿɵõ��Ͳ�������ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�������ABC�Ķ�������Ϊ��A��1��2����B��2����1����C��4��3����
��1����������ABC����ƽ��5����λ���ȣ�������ƽ��2����λ���ȣ���������A'B'C'������������A'B'C'����д��������A'B'C'�Ķ������ꣻ
��2��ֱ��д��������A'B'C'����� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��AB=6����E�ڱ�CD�ϣ�CE=2DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����EG=DE+BG����AG��CF����S��FCA=3.6��������ȷ������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��27�ľ��루B��F��C��һ��ֱ���ϣ���

��1����칫¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ��룮
���ο����ݣ�sin22����![]() ��cos22����
��cos22����![]() ��tan22����
��tan22����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() Ϊ����
����![]() ��
��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��
��![]() ��������
��������![]() ��������ۢ�
��������ۢ�![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ����ǣ�_____________��ֻ����ţ�
��������ȷ�Ľ����ǣ�_____________��ֻ����ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com