
����Ŀ��ij���Ͳ�������ͬ�����µķ�ѿʵ�������±���
ÿ������n | 100 | 150 | 200 | 500 | 800 | 1 000 |
��ѿ������m | 65 | 111 | 136 | 345 | 560 | 700 |
��ѿ��Ƶ�� | 0.65 | 0.74 | 0.68 | 0.69 | a | b |
��1��a�� ��b�� ��
��2�������Ͳ��ѷ�ѿ�ĸ��ʹ���ֵ�Ƕ��٣����Ҫ˵�����ɣ�
��3����������Ͳ��ѷ�ѿ��ij�����Ϊ90%��������ͬ��������10 000�������Ͳ��ѿɵõ��Ͳ�������ٿã�
���𰸡���1��0.70��0.70����2��0.70����3��6 300��
��������
��1���÷�ѿ��������ÿ�������������a��b��ֵ��
��2����������ͬ�����£����ʵ�飬ijһ�¼��ķ���Ƶ�ʽ��Ƶ��ڸ��ʼ��ɵó��𰸣�
��3�������������Է�ѿ���ٳ��Գ����ʼ��ɣ�
��1��a=![]() =0.70��
=0.70��
b=![]() =0.70��
=0.70��
��2���߷�ѿ��Ƶ�ʽӽ�0.70,
����ʹ���ֵΪ0.70��
���ɣ�����ͬ�����£����ʵ�飬ijһ�¼��ķ���Ƶ�ʽ��Ƶ��ڸ��ʣ�
��3��10000��0.70��90%��6300�����
������ͬ��������10000�������Ͳ��ѿɵõ��Ͳ�����6300�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
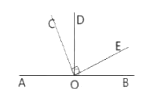
����Ŀ����ͼ����ֱ��![]() ��һ��
��һ��![]() ����
����![]() ��
��![]() ����
����![]() �����㻹�������Щ�ǵĶ���_____________________������д��������ֱ�Ǻ�ƽ�dz��⣩��
�����㻹�������Щ�ǵĶ���_____________________������д��������ֱ�Ǻ�ƽ�dz��⣩��
����![]() ����Ľ���__________�����ǵ�������ϵ��________���ɴ���ó��Ľ�����_____________________.
����Ľ���__________�����ǵ�������ϵ��________���ɴ���ó��Ľ�����_____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ10�� AB=16, ��B��A�����,����P�ӵ�A��������ÿ��3����λ���ٶ����������������˶������˶�ʱ��Ϊt(t>0����.
��1��д�������ϵ�B��ʾ����_______
��2���߶�AP�ij�Ϊ________���ú�t�Ĵ���ʽ��ʾ��
��3��������Q��B��������ÿ��1����λ���ٶ����������������˶�����P,Qͬʱ���������˶�������ʱ��P��Q����?
��4��������Q��B��������ÿ��1����λ���ٶ����������������˶�����P,Qͬʱ������ ���P�˶�������ʱ�ϵ�Q?
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
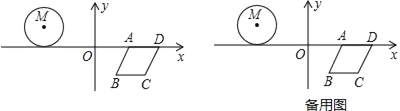
����Ŀ����ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ����3��1������A������Ϊ��2��0������B������Ϊ��1����![]() ������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
��1��������ABCD���ܳ���
��2������M��x��������ÿ��2����λ���ȵ��ٶ�ƽ�ƣ�����ABCD��x��������ÿ��3����λ���ȵ��ٶ�ƽ�ƣ��������ƶ���ʱ��Ϊt���룩������M��AD���У����е�ΪAD���е�ʱ������AC����t��ֵ����MAC�Ķ�����
��3���ڣ�2���������£�����M��AC���ڵ�ֱ�ߵľ���Ϊ1ʱ����t��ֵ��
���𰸡���1�����ε��ܳ�Ϊ8����2��t=![]() ����MAC=105������3����t=1��
����MAC=105������3����t=1��![]() ��t=1+
��t=1+![]() ʱ��ԲM��AC���У�
ʱ��ԲM��AC���У�
�������������������1������B��BE��AD������ΪE���ɵ�A�͵�B�������֪��BE=![]() ��AE=1�����ݹ��ɶ��������AB�ij����Ӷ���������ε��ܳ�����2���� M��x�������ΪF��AD���е�ΪE�������EF�ij���Ȼ�����·��=ʱ�����ٶ��г����̼��ɣ�ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ M��AD���е㣮������������Ǻ���ֵ����á�EAB=60�����������ε����ʿɵõ���FAC=60����Ȼ��֤����AFM�ǵ���ֱ�������Σ��Ӷ��ɵõ���MAF�Ķ������ʴ˿���á�MAC�Ķ�������3����ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE������á�MAE=30������������������Ǻ���ֵ�ɵõ�AE�ij���Ȼ������3t+2t=5-AE�����t��ֵ����ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE���������ε����ʺ����߳���������á�MAE=60����Ȼ����������������Ǻ���ֵ�ɵõ�EA=
��AE=1�����ݹ��ɶ��������AB�ij����Ӷ���������ε��ܳ�����2���� M��x�������ΪF��AD���е�ΪE�������EF�ij���Ȼ�����·��=ʱ�����ٶ��г����̼��ɣ�ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ M��AD���е㣮������������Ǻ���ֵ����á�EAB=60�����������ε����ʿɵõ���FAC=60����Ȼ��֤����AFM�ǵ���ֱ�������Σ��Ӷ��ɵõ���MAF�Ķ������ʴ˿���á�MAC�Ķ�������3����ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE������á�MAE=30������������������Ǻ���ֵ�ɵõ�AE�ij���Ȼ������3t+2t=5-AE�����t��ֵ����ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE���������ε����ʺ����߳���������á�MAE=60����Ȼ����������������Ǻ���ֵ�ɵõ�EA=![]() ���������3t+2t=5+AE���з�����⼴�ɣ�
���������3t+2t=5+AE���з�����⼴�ɣ�
����������� ![]() ����ͼ1��ʾ������
����ͼ1��ʾ������![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��

��![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
���ı���![]() Ϊ���Σ�
����
��![]() ��
��
�����ε��ܳ�![]() ��
��
��![]() ����ͼ2��ʾ����
����ͼ2��ʾ����![]() ��
��![]() �������Ϊ
�������Ϊ![]() ��
�� ![]() �е�Ϊ
�е�Ϊ![]() ��
��

��![]() ��
��
��![]() ��
��
��![]() ����
����![]() Ϊ
Ϊ![]() �е㣬
�е㣬
��![]() ��
�� ![]() ��
��
��![]() ��
��
���![]() ��
��
ƽ�Ƶ�ͼ����ͼ3��ʾ������![]() ��
��![]() ��
��

����Ϊ![]() ������
������![]() ��
�� ![]() ��
��![]() ��
��![]() �е㣬
�е㣬
���ɣ�![]() ����֪��
����֪�� ![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() �����Σ�
������
��![]() ��
��
��![]() Ϊ
Ϊ![]() ���ߣ�
���ߣ�
��![]() ��
��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
��![]() ��
��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��![]() ��
��
��![]() ��
��
��![]() ����ͼ4��ʾ������
����ͼ4��ʾ������![]() ��������
��������![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��

���ı���![]() Ϊ���Σ�
���� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��Բ
��Բ![]() ������
������
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ͼ5��ʾ������![]() ��������
��������![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��

���ı���![]() Ϊ���Σ�
���� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��Բ
��Բ![]() �����ߣ�
�����ߣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
������������![]() ��
��![]() ʱ��Բ
ʱ��Բ![]() ��
��![]() ����
����
�㾦��������һ��Բ���ۺ���.Բ�еķ��������ܽ1����������˼�룺�о��㡢ֱ�ߺ�Բ��λ�ù�ϵʱ����Ҫ�Ӳ�ͬ��λ�ù�ϵȥ���ǣ���Ҫȫ���ʾ�㡢ֱ�ߺ�Ԫ�ĸ��ֿ��ܵ�λ�ù�ϵ.����λ�ù�ϵ�Ŀ��������Ҫ�õ���������˼��.1��ת��˼�룺��1���������桱Ϊ��ƽ�桱��2����������ͼ�����Ϊ����ͼ�ε�������.3������˼�룺����Բ�йصļ������У�����ֱ�����ù�ʽ���м����⣬��ʱ����ͼ�ε��ص㣬�з��̽��˼·��������̼��.
�����͡������
��������
28
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��x�ᡢy��ֱ��ڵ�B��4��0����C��0��3������AΪx�Ḻ������һ�㣬AM��BC�ڵ�M��y���ڵ�N��0�� ![]() ������֪������y=ax2+bx+c������A��B��C��
������֪������y=ax2+bx+c������A��B��C��

��1���������ߵĺ���ʽ��
��2������AC����D���߶�BC�Ϸ����������ϣ�����DC��DB������BCD����ABC�������S��BCD= ![]() S��ABC�� ���D�����ꣻ
S��ABC�� ���D�����ꣻ
��3����ͼ2��EΪOB�е㣬��FΪ�߶�BC��һ�㣨�����˵㣩������EF��һ����P��E���������߶�EF��ÿ��3����λ���ٶ��˶���F���������߶�PC��ÿ��5����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ͼ�У�ֱ�߶�����һ�㣬��̽������-һ���ֱ�ߵ����������γɵĶԶ��ǵĶ���֮��Ĺ��ɡ�
(1)��۲���ͼ����д�±�
����һ���ֱ�ߵ����� | 2 | 3 | 4 |
�Զ��ǵĶ��� |
(2)��n��ֱ�߽���һ�㣬����_____________�ԶԶ���(�ú�n�Ĵ���ʽ��ʾ).
(3)��100��ֱ�߽���һ��ʱ������_____________�ԶԶ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵������abc��0����2a��b=0����4a+2b+c��0����������5��y1������![]() ��y2���������������㣬��y1��y2��
��y2���������������㣬��y1��y2��
����˵����ȷ���ǣ�������

A. �٢� B. �ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��������һ�ܿ����Ķ�ʱ��������������ȡ������ѧ�����е��飬���ݵ����������Ķ�ʱ����Ϊ���ࣺ2Сʱ���ڣ�2��4Сʱ����2Сʱ����4��6Сʱ����4Сʱ����6Сʱ�����ϣ�����������ͼ��ʾ��������ͳ��ͼ��

��1�����ε��鹲�����ȡ�� ��ѧ����
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�У������Ķ�ʱ����4��6Сʱ����Ӧ��Բ�ĽǶ���Ϊ ![]() ��
��
��4������������10 000�������������Ƹõ�����ѧ��һ�ܿ����Ķ�ʱ��������4Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() ��Ҫʹ�ı���
��Ҫʹ�ı���![]() ��ƽ���ı��Σ����п����ӵ���������ȷ���ǣ� ��
��ƽ���ı��Σ����п����ӵ���������ȷ���ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��������������A(��1��0)��B(��2����2)��C(��4����1)��
��1���뻭����ABC��������ԭ��O�����ĶԳ�ͼ����A1B1C1����д����A1B1C1���������������
��2����ֱ��д��������������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D����������������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com