
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ),则称点
),则称点![]() 为点
为点![]() 的“
的“![]() 属派生点”.例如:
属派生点”.例如:![]() 的“2属派生点”为
的“2属派生点”为![]() ,即
,即![]() .
.
(l)求点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标:
的坐标:
(2)若点![]() 的“5属派生点”
的“5属派生点”![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标:
的坐标:
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的“收属派生点”为
的“收属派生点”为![]() 点,且线段
点,且线段![]()
![]() 的长度为线段
的长度为线段![]() 长度的2倍,求k的值.
长度的2倍,求k的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据“k属派生点”计算可得;
(2)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(3)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
解:(1)点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标为
的坐标为![]() ,即
,即![]()
(2)设![]() ,
,
依题意,得方程组:![]() ,
,
解得![]() ,.
,.
∴点![]()
(3)∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka)
∴线段PP′的长为P′到x轴距离为|ka|.
∵P在x轴正半轴,线段OP的长为a,
∴|ka|=2a,即|k|=2,
∴k=±2.


科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
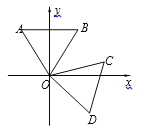
【题目】如图,等边△OAB的顶点O为坐标原点,AB∥x轴,OA=2,将等边△OAB绕原点O顺时针旋转105至△OCD的位置,则点D的坐标为( )
A.(2,-2)B.(![]() ,
,![]() )C.(
)C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为10, AB=16, 且B在A的左侧,动点P从点A出发,以每秒3个单位的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数_______
(2)线段AP的长为________(用含t的代数式表示)
(3)若动点Q从B出发,以每秒1个单位的速度沿数轴向右匀速运动,若P,Q同时出发,求运动多少秒时,P、Q相遇?
(4)若动点Q从B出发,以每秒1个单位的速度沿数轴向左匀速运动,若P,Q同时出发, 求点P运动多少秒时追上点Q?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
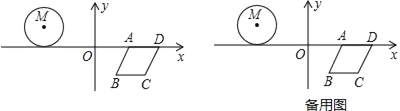
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣![]() ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值.
【答案】(1)菱形的周长为8;(2)t=![]() ,∠MAC=105°;(3)当t=1﹣
,∠MAC=105°;(3)当t=1﹣![]() 或t=1+
或t=1+![]() 时,圆M与AC相切.
时,圆M与AC相切.
【解析】试题分析:(1)过点B作BE⊥AD,垂足为E.由点A和点B的坐标可知:BE=![]() ,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=
,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=![]() ,最后依据3t+2t=5+AE.列方程求解即可.
,最后依据3t+2t=5+AE.列方程求解即可.
试题解析:( ![]() )如图1所示:过点
)如图1所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,

∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∴菱形的周长![]() .
.
(![]() )如图2所示,⊙
)如图2所示,⊙![]() 与
与![]() 轴的切线为
轴的切线为![]() ,
, ![]() 中点为
中点为![]() ,
,

∵![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() 为
为![]() 中点,
中点,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
解得![]() .
.
平移的图形如图3所示:过点![]() 作
作![]() ,
,

垂足为![]() ,连接
,连接![]() ,
, ![]() 为⊙
为⊙![]() 与
与![]() 切点,
切点,
∵由(![]() )可知,
)可知, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() 为
为![]() 切线,
切线,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
(![]() )如图4所示:连接
)如图4所示:连接![]() ,过点作
,过点作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,
,

∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() .
.
∵![]() 、
、![]() 是圆
是圆![]() 的切线
的切线
∴![]() ,
,
∵![]() 。
。
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图5所示:连接![]() ,过点作
,过点作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,
,

∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 是圆
是圆![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,当![]() 或
或![]() 时,圆
时,圆![]() 与
与![]() 相切.
相切.
点睛:此题是一道圆的综合题.圆中的方法规律总结:1、分类讨论思想:研究点、直线和圆的位置关系时,就要从不同的位置关系去考虑,即要全面揭示点、直线和元的各种可能的位置关系.这种位置关系的考虑与分析要用到分类讨论思想.1、转化思想:(1)化“曲面”为“平面”(2)化不规则图形面积为规则图形的面积求解.3、方程思想:再与圆有关的计算题中,除了直接运用公式进行计算外,有时根据图形的特点,列方程解答,思路清楚,过程简捷.
【题型】解答题
【结束】
28
【题目】如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, ![]() ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.

(1)求抛物线的函数式;
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= ![]() S△ABC, 求点D的坐标;
S△ABC, 求点D的坐标;
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各图中,直线都交于一点,请探究交于-一点的直线的条数与所形成的对顶角的对数之间的规律。
(1)请观察上图并填写下表
交于一点的直线的条数 | 2 | 3 | 4 |
对顶角的对数 |
(2)若n条直线交于一点,则共有_____________对对顶角(用含n的代数式表示).
(3)当100条直线交于一点时,则共有_____________对对顶角

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.

(1)本次调查共随机抽取了 名学生;
(2)补全条形统计图;
(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ![]() ;
;
(4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的伯,解容下列问题
(I)放入一个小球水面升高____cm,放入一个大球水面升高_____cm
(2)如果放入10个球,使水面上升到50cm,应放入大球、小像各多少个?
(3)現放入干个球,使水面升高2lcm,且小球个数为偶数个,问有几种可能,请一一列出(写出结果即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com