
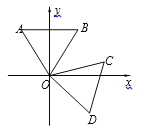
【题目】如图,等边△OAB的顶点O为坐标原点,AB∥x轴,OA=2,将等边△OAB绕原点O顺时针旋转105至△OCD的位置,则点D的坐标为( )
A.(2,-2)B.(![]() ,
,![]() )C.(
)C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
【答案】D
【解析】
过点D向x轴作垂线,垂足为E,根据等边三角形的性质以及直线平行的性质证明△EOD是等腰直角三角形,再根据等边三角形的边长以及D点在第四象限即可得到答案.
解:如图,过点D向x轴作垂线,垂足为E,

∵△OAB是等边三角形,旋转角是105°,
∴∠AOB=∠B=∠COD =60°,∠AOC=105°,
∴∠BOC=∠AOC-∠AOB=105°-60°=45°,
又∵AB∥x轴,
∴∠BOE=∠B=60°(两直线平行,内错角相等),
∴∠COE=∠BOE-∠BOC=60°-45°=15°,
∴∠EOD=∠DOC-∠COE=60°-15°=45°,
∴△EOD是等腰直角三角形,
∴![]()
∵OD=OA=2,
∴![]() (勾股定理),
(勾股定理),
∴![]()
∵D点在第四象限,
∴D点的坐标为:(![]() ,
,![]() )
)
故选D;


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对本校甲、乙两班各60名学生进行了垃极分类相关知识的测试,并分别随机抽取了15份成绩,整理分析过程如下,请补充完整
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
按如下分数段整理、描述这两组样本数据
组别 班级 | 65.6~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲班 | 2 | 2 | 4 | 5 | 1 | 1 |
乙班 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲班 | 80 | x | 80 | 47.6 |
乙班 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(2)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类相关知识合格的学生有 人
(3)你认为哪个班的学生掌握垃圾分类相关知识的情况较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
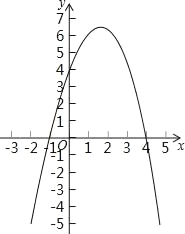
【题目】已知二次函数y=﹣x2+3x+4的图象如图:(直接写答案)
(1)方程﹣x2+3x+4=0的解是 ;
(2)不等式﹣x2+3x+4>0的解集是 ;
(3)不等式﹣x2+3x+4<0的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,OC平分∠AOB,在直线AB另一端以O为顶点作∠DOE=900。

(1) 若∠AOE=480,求∠BOD的度数。
(2) 写出图中与∠AOE互余的角。
(3) ∠AOE与∠COD有什么数量关系,请写出你的结论并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.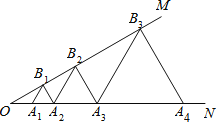
查看答案和解析>>
科目:初中数学 来源: 题型:
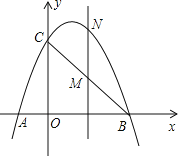
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ),则称点
),则称点![]() 为点
为点![]() 的“
的“![]() 属派生点”.例如:
属派生点”.例如:![]() 的“2属派生点”为
的“2属派生点”为![]() ,即
,即![]() .
.
(l)求点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标:
的坐标:
(2)若点![]() 的“5属派生点”
的“5属派生点”![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标:
的坐标:
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的“收属派生点”为
的“收属派生点”为![]() 点,且线段
点,且线段![]()
![]() 的长度为线段
的长度为线段![]() 长度的2倍,求k的值.
长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com