
【题目】如图,E,F分别是等边△ABC边AB,AC上的点,且AE=CF,CE,BF交于点P.
(1)证明:CE=BF;
(2)求∠BPC的度数.

【答案】(1)见解析;(2)∠BPC=120°.
【解析】
(1)欲证明CE=BF,只需证得△BCE≌△ABF;
(2)利用(1)中的全等三角形的性质得到∠BCE=∠ABF,则由图示知∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,所以根据三角形内角和定理求得∠BPC=120°.
证明:(1)∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
 ,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标A(-1,0)、B(-2,-2)、C(-4,-1).
(1)请画出△ABC关于坐标原点O的中心对称图形△A1B1C1,并写出△A1B1C1的面积 .
(2)请直接写出:所有满足以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() .把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.
.把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(3ab)2(﹣![]() ab3)
ab3)
(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
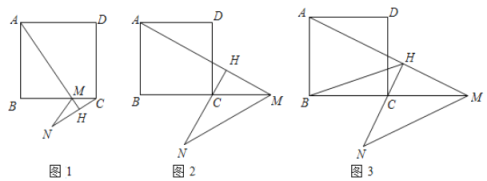
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,AB=10,AO=6,BO=8,则下列结论中,错误的是( ) .
A.AC⊥BDB.四边形ABCD是菱形
C.AC=BCD.△ABO≌△CDO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com