【题目】如图，在平面直角坐标系中，
，
，
，
．把一条长为2019个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A-B-C-D-A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是__________.
53天天练系列答案科目：初中数学 来源： 题型：
【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高3米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有27米的距离（B，F，C在一条直线上）．
（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．
（参考数据：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
材料1：对于一个关于
的二次三项式
，除了可以利用配方法求请多项式的取值范围外，爱思考的小川同学还想到了其他的方法：比如先令
，然后移项可得：
，再利用一元二次方程根的判别式来确定
的取值范围，请仔细阅读下面的例子：
例：求
的取值范围：
解：令
∴
∴
∴
∴
；
材料2：在学习完一元二次方程的解法后，爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题，他的具体做法如下：
若关于的一元二次方程
（
）有两个不相等的实数根
，
（
）
则关于的一元二次不等式
（）的解集为：
或
．
则关于的一元二次不等式
（）的解集为：
．
请根据上述材料，解答下列问题：
（1）若关于的二次三项式
（
为常数）的最小值为－6，则
________；
（2）求出代数式
的取值范围；
（3）若关于的代数式
（其中
、
为常数，且
）的最小值为－4，最大值为7，请求出满足条件的，的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是圆O的弦，OA⊥OD，AB，OD相交于点C，且CD=BD．
（1）判断BD与圆O的位置关系，并证明你的结论；
（2）当OA=3，OC=1时，求线段BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB，CD边于点E，F.
（1）求证：四边形DEBF是平行四边形；
（2）当四边形DEBF是菱形时，求菱形的周长．
（3）在（2）的基础上，直接写出BD与EF的位置关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人.
使用手机的目的 每周使用手机的时间
（0~1表示大于0同时小于等于1，以此类推）
请你根据以上信息解答下列问题：
（1）在扇形统计图中，“玩游戏”对应的百分比为_______，圆心角度数是度_______；
（2）补全条形统计图：
（3）该校共有学生2100人，估计每周使用手机时间在2小时以上（不含2小时）的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=
在同一坐标系内的图象大致为（ ）
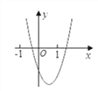
A. 
B. 
C. 
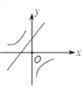D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
