
【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
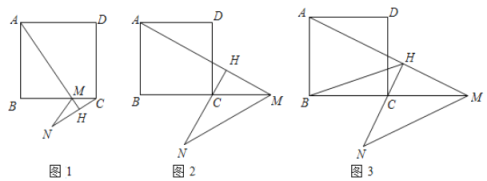
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)BH=![]() .
.
【解析】
(1)利用平行线的性质以及三角形的外角的性质证明即可.
(2)如图2中,延长MN,AB交于点K,连接CK,只要证明△AMB≌△KMB(ASA),CN=KN即可解决问题.
(3)如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.想办法证明BC=CM,推出tan∠AMB=tan∠BMK=![]() ,解直角三角形求出HF,BF即可解决问题.
,解直角三角形求出HF,BF即可解决问题.
(1)证明:如图1中,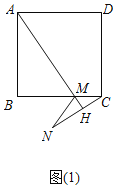
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAH=∠AMB,
∵∠AMB=∠NMB,∠NMB=∠N+∠NCB,
∴∠DAH=∠N+∠NCB.
(2)证明:如图2中,延长MN,AB交于点K,连接CK,CA.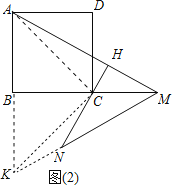
在正方形ABCD中,∠ABC=90°,AD∥BC,
∵∠AMB=∠BMN,
∵∠ABM=∠KBM=90°,BM=BM,
∴△AMB≌△KMB(ASA),
∴BK=AB=BC,∠BKM=∠BAM,AM=KM,
∴∠BKC=∠BCK,
∵CH⊥AM,
∴∠BAM=90°-∠AMB=90°-∠CMH=∠BCN,
∴∠BKM=∠BCN,
∴∠BKC-∠BKM=∠BCK-∠BCN,
∴∠NKC=∠NCK,
∴NK=NC,
∵KM=MN+NK,
∴AM=MN+CN.
(3)解:如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.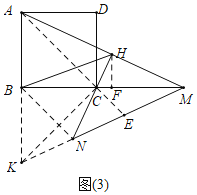
设CN=KN=x,则MN=2x,
∵BK=BC,BN=BN,KN=KC,
∴△BNK≌△BNC(SSS),
∴∠NBK=∠NBC=![]() ∠CBK=45°,
∠CBK=45°,
∵四边形ABC都是正方形,
∴∠BAC=45°,
∴∠NBK=∠BAC,
∴AE∥BN,
∵AB=BK,
∴KN=NE=x,
∴EN=EM=x,
∵CE∥BN,EN=EM,
∴BC=CM,
∴tan∠AMB=tan∠BMK=![]() =
=![]() ,
,
在Rt△CHM中,∵∠CHM=90°,
∴tan∠CMH=![]() ,
,
∵CH=2![]() ,
,
∴MH=4![]() ,
,
∴CM=![]() =10,
=10,
∵![]() CHHM=
CHHM=![]() CMHF,
CMHF,
∴FH=4,FM=8,CF=2,
在Rt△BHF中,BH=![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]()
![]() ,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令![]()
![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围:
的取值范围:
解:令![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )有两个不相等的实数根
)有两个不相等的实数根![]() ,
,![]() (
(![]() )
)
则关于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集为:
)的解集为:![]() 或
或![]() .
.
则关于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集为:
)的解集为:![]() .
.
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为-6,则
为常数)的最小值为-6,则![]() ________;
________;
(2)求出代数式![]() 的取值范围;
的取值范围;
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为-4,最大值为7,请求出满足条件的
)的最小值为-4,最大值为7,请求出满足条件的![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
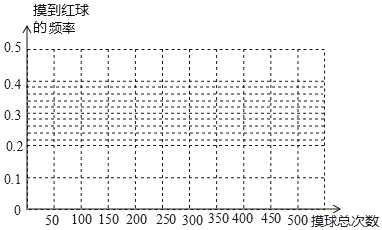
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式![]() +(b-3)2=0,(c-4)2≤0.
+(b-3)2=0,(c-4)2≤0.
(1)求a,b,c的值;
(2)求出三角形ABC的面积?
(3)如果在第二象限内有一点P(m,![]() ),那么请用含m的式子表示四边形ABOP的面积;
),那么请用含m的式子表示四边形ABOP的面积;
(4)在(3)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
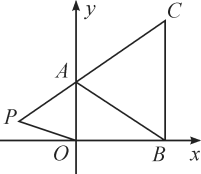
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
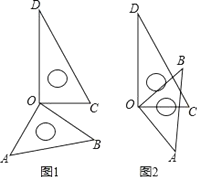
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
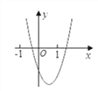
A.  B.
B.  C.
C. 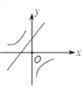 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感恩节即将来临,小王调查了初三年级部分同学在感恩节当天将以何种方式对帮助过自己的人表达感谢,他将调查结果分为如下四类:A类﹣﹣当面表示感谢、B类﹣﹣打电话表示感谢、C类﹣﹣发短信表示感谢、D类﹣﹣写书信表示感谢.他将调查结果绘制成了如图所示的扇形统计图和条形统计图.请你根据图中提供的信息完成下列各题:
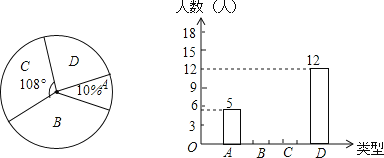
(1)补全条形统计图;
(2)在A类的同学中,有4人来自同一班级,其中有2人主持过班会.现准备从他们4人中随机抽出两位同学主持感恩节主题班会课,请用树状图或列表法求抽出1人主持过班会而另一人没主持过班会的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com