
����Ŀ��һ�������������������ֲ�������̽�����������������Ĺ��̣�������һ��������������һ��.
�����ֲ��룩��1����ͼ�٣���֪��AOB��70������AOD��100����OCΪ��BOD�Ľ�ƽ���ߣ����AOC�Ķ���Ϊ ��.
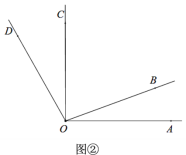
��̽�����ɣ���2����ͼ�٣���AOB��m����AOD��n��OCΪ��BOD�Ľ�ƽ����. �����AOC�Ķ������ú�m��n�Ĵ���ʽ��ʾ������˵������.
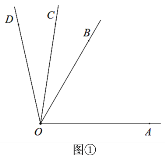
������������3����ͼ�ڣ�����AOB��20������AOC��90������AOD��120��.������OB�Ƶ�O��ÿ��20����ʱ����ת������OC�Ƶ�O��ÿ��10��˳ʱ����ת������OD�Ƶ�Oÿ��30��˳ʱ����ת����������ͬʱ��ת����һ��������ֱ��OA�غ�ʱ����������ͬʱֹͣ�˶�. �˶�����ʱ������һ�������������������нǵĽ�ƽ���ߣ�
���𰸡���1��85������2����AOC��![]() �����ɼ���������3������
�����ɼ���������3������![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.
��������
��1�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ�������BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ����������BOC�Ķ������ټ����AOC���ɽ������.
��2�����ݡ�AOD����AOB����BOD֮��Ĺ�ϵ����m��n��ʾ����BOD�Ķ�����Ȼ����ݽ�ƽ���ߵ�������m��n�Ĵ���ʽ��ʾ����BOC������ٱ�ʾ����AOC���ɽ������.
��3�����ݸ���֮����ڵ�������ϵ���辭��x��ʱ���ֱ���x����DOA����COA����BOA��ʾ������Ȼ�������������ۣ����ݽ�ƽ���ߵ������г����̣��������.
��1��85����
��2���ߡ�AOB��m����AOD��n
���BOD��n��m
��OCΪ��BOD�Ľ�ƽ����
���BOC��![]()
���AOC��![]() +m��
+m��![]()
��3���辭����ʱ��Ϊx�룬
���DOA��120����30x����COA��90����10x����BOA��20��+20x��
�ٵ���x��![]() ֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
֮ǰ��OCΪOB��OD�Ľ�ƽ���ߣ�30��20x��70��30x��x1��4���ᣩ��
�ڵ�x��![]() ��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��
��2֮�䣬ODΪOC��OB�Ľ�ƽ���ߣ���30+20x��100��50x��x2��![]() ��
��
�۵�x��2��![]() ֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��
֮�䣬OBΪOC��OD�Ľ�ƽ���ߣ�70��30x����100+50x��x3��![]() ��
��
�ܵ�x��![]() ��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
��4֮�䣬OCΪOB��OD�Ľ�ƽ���ߣ���70+30x����30+20x��x4��4.
�𣺾���![]() ��
��![]() ��4��ʱ������һ�������������������нǵ�ƽ����.
��4��ʱ������һ�������������������нǵ�ƽ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�������������ƻ���һ����ʱ��������̻����![]() ��Ķ��������������������ԭ���ƻ��������̻����Ҫ��ԭ�ƻ��Ļ���������
��Ķ��������������������ԭ���ƻ��������̻����Ҫ��ԭ�ƻ��Ļ���������![]() ������Ҫ��ǰ
������Ҫ��ǰ![]() �������������Ҫ����µļƻ���ƽ��ÿ����̻���������ԭ�ƻ���
�������������Ҫ����µļƻ���ƽ��ÿ����̻���������ԭ�ƻ���![]() ��Ķ����ԭ�ƻ�ƽ��ÿ����̻������
��Ķ����ԭ�ƻ�ƽ��ÿ����̻������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�������������궼�ڸ���ϣ��ҡ�A1B1C1���ABC����ԭ��O�����ĶԳƣ�C������Ϊ��-2,1����
��1����ֱ��д��A1�������� ������������A1B1C1��
��2��P��a��b���ǡ�ABC��AC����һ�㣬����ABCƽ�ƺ��P�ĶԳƵ�P'��a+2��b��6�����뻭��ƽ�ƺ�ġ�A2B2C2��
��3������A1B1C1�͡�A2B2C2����ijһ������ĶԳƣ���Գ����ĵ�����Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,AD��Rt��ABCб��BC�ϵĸ�.
��1���߹���ͼ:����C��ƽ����,��AB�ڵ�E,��AD�ڵ�F����д����,���뱣����ͼ�ۼ�,����Ӧ�е���ĸ��;
��2���ڣ�1����������,��F��BC��ƽ���߽�AC�ڵ�H,�߶�FH���߶�CH��������ϵ���?������֤��;
��3���ڣ�2����������,����DEDH.��֤:ED��HD.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶��ѧ��ȤС�飬�ڹ㳡�ϲ���λ�����������ij������AC�ĸ߶ȣ���ͼ��ʾ�������ڵ�B��øý����ﶥ��A������Ϊ30����Ȼ������������ǰ��62�ף�����D�㣬�ٲ�øý����ﶥ��A������Ϊ60�㣨B��C��D������ͬһˮƽ���ϣ��Ҳ����ǵĸ߶Ⱥ��Բ��ƣ�����ý�����AC�ĸ߶ȣ������ȷ��1�ף��ο���ֵ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��10��17�����ҹ����������ƶ����,ijУѧ����ɲ���ѧ������������ƶ����Ը������г�������,�õ�һ��ѧ��������������,��ѧУ���־���������е���ͷ���ͳ�ƺ�,��������������ͼ��ʾ��ͳ��ͼ,(ͼ����Ϣ������)����֪A.B�����������ı�Ϊ1:5.

������ľ����������ͳ�Ʊ���
��� | ����x/Ԫ | ���� |
A | 1��x��10 | a |
B | 10��x��20 | 100 |
C | 20��x��30 | ______ |
D | 30��x��40 | ______ |
E | 40��x | ______ |
����������Ϣ����������⣺
(1)��a��ֵ�Ͳ���������������
(2)��ȫ��������ľ����������ͳ��ͼ1������������B��Բ�ĽǶ�����
(3)��֪��У��ѧ��2200�ˣ�����ƾ����������30Ԫ��ѧ�������ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ�������ó˷�����ʦ��ͬѧ������һ����Ŀ��
���㣺49![]() ������5������˭����ֿ��ֶԣ�����λͬѧ�Ľⷨ���£�
������5������˭����ֿ��ֶԣ�����λͬѧ�Ľⷨ���£�
�ϴϣ�ԭʽ=��![]() ��5=��
��5=��![]() =��249
=��249![]() ��
��
������ԭʽ=��49+![]() ��������5��=49������5��+
��������5��=49������5��+![]() ������5��=��249
������5��=��249![]() ��
��
��1�������������ֽⷨ������Ϊ˭�Ľⷨ�Ϻã�
��2������Ľⷨ�����к�����������Ϊ���и��õķ���������У������д������
��3��������Ϊ����ʵķ������㣺29![]() ������8��
������8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��kx+k��2�����㣨m��n+1���ͣ�m+1��2n+3�����ҩ�2��k��0����n��ȡֵ��Χ�ǣ�������
A. ��2��n��0B. ��4��n����2C. ��4��n��0D. 0��n����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣���ͼ��ֱ��l������A��1��6���͵�B����3����2����

��1����ֱ��l�Ľ���ʽ��ֱ����������Ľ������ꣻ
��2�����AOB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com