
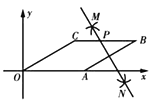
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.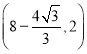 C.
C.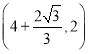 D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),已知
左侧),已知![]() 点的纵坐标是2.
点的纵坐标是2.
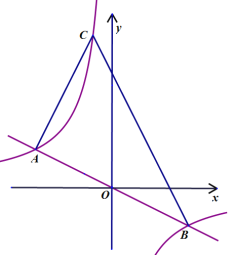
(1)求反比例函数的表达式;
(2)点![]() 上方的双曲线上有一点
上方的双曲线上有一点![]() ,如果
,如果![]() 的面积为30,直线
的面积为30,直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
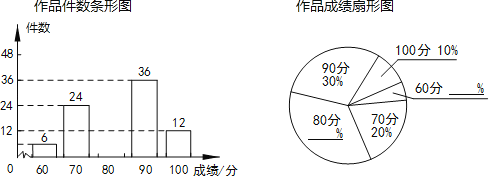
【题目】3月5日是学雷锋日,某校组织了以“向雷锋同志学习”为主题的小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.根据以下信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共1200份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西柳州市)如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足![]() =PAPC,连接CE,AE,OE,OE交CA于点D.
=PAPC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP=![]() AC,求证:DO=DP.
AC,求证:DO=DP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
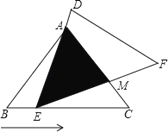
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由;
(3)求当线段AM最短时的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象相交于点
的图象相交于点![]() 和
和![]() .
.

(1)求一次函数和反比例函数的解析式;
(2)若定义横、纵坐标均为整数的点叫做好点,则图中阴影部分区域内(不含边界)好点的个数为________;
(3)请根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
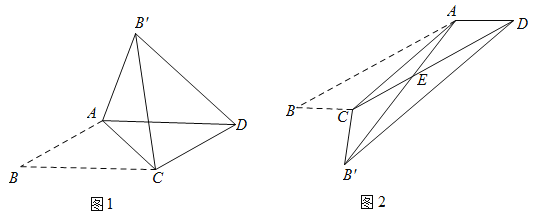
【题目】我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现与证明)![]() ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
结论1:B′D∥AC;
结论2:△AB′C与![]() ABCD重叠部分的图形是等腰三角形.
ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2(只需证明一个结论).
(应用与探究)在![]() ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
(1)如图1,若![]() ,则∠ACB= °,BC= ;
,则∠ACB= °,BC= ;
(2)如图2,![]() ,BC=1,AB′与边CD相交于点E,求△AEC的面积;
,BC=1,AB′与边CD相交于点E,求△AEC的面积;
(3)已知![]() ,当BC长为多少时,是△AB′D直角三角形?
,当BC长为多少时,是△AB′D直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com