
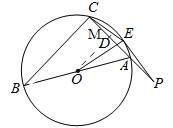
【题目】(2016广西柳州市)如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足![]() =PAPC,连接CE,AE,OE,OE交CA于点D.
=PAPC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP=![]() AC,求证:DO=DP.
AC,求证:DO=DP.

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)利用两边对应成比例,夹角相等,两三角形相似即可;
(2)连接BE,转化出∠OEB=∠PCE,又由相似得出∠PEA=∠PCE,从而用直径所对的圆周角是直角,转化出∠OEP=90°即可;
(3)构造全等三角形,先找出OD与PA的关系,再用等积式找出PE与PA的关系,从而判断出OM=PE,得出△ODM≌△PDE即可.
(1)∵![]() =PAPC,
=PAPC,
∴![]() ,
,
∵∠APE=∠EPC,
∴△PAE∽△PEC;
(2)如图1,连接BE,
∴∠OBE=∠OEB,
∵∠OBE=∠PCE,
∴∠OEB=∠PCE,
∵△PAE∽△PEC,
∴∠PEA=∠PCE,
∴∠PEA=∠OEB,
∵AB为直径,∴∠AEB=90°,
∴∠OEB+∠OEA=90°,
∵∠PEA+∠OEA=90°,
∴∠OEP=90°,
∵点E在⊙O上,
∴PE是⊙O的切线;

(3)如图2,过点O作OD⊥AC于M,
∴AM=![]() AC,
AC,
∵BC⊥AC,
∴OD∥BC,
∵∠ABC=30°,
∴∠AOD=30°,
∴OD=![]() AM=
AM=![]() AC,
AC,
∵AP=![]() AC,
AC,
∴OD=![]() AP,
AP,
∵PC=AC+AP=2AP+AP=3AP,
∴![]() =PA×PC=PA×3PA,
=PA×PC=PA×3PA,
∴PE=![]() PA,
PA,
∴OD=PE,
∵∠PED=∠OMD=90°,∠ODM=∠PDE,
∴△ODM≌△PDE,
∴OD=DP.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题.
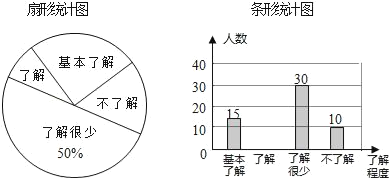
(1)接受问卷调查的学生共有 名,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;请补全条形统计图;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解””和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
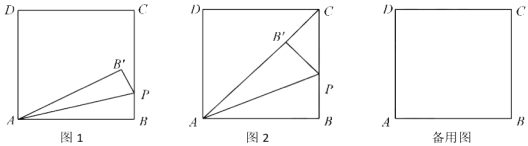
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.﹣1≤t≤0B.﹣1≤t![]() C.
C.![]() D.t≤﹣1或t≥0
D.t≤﹣1或t≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
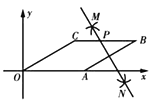
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.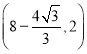 C.
C.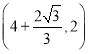 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
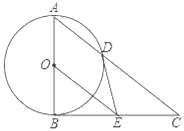
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com